本课程是MITx在线数学课之一,是系列课程XSeries in 18.03x Differential Equations的第一个,也是学习后续高阶课的必修基础课,名为Introduction to Differential Equation 代号18.031x。整个系列未看到中文版。课程由来自麻省理工、普林斯顿等大学的多位教授、研究人员设计制作, 是一套非常棒的课程,内容丰满、制作精良。18.031x共有五个单元。本系列博客是经过我自己翻译后的中文笔记。
$$ \Large Unit 3:\ Damped\ Oscillation $$
6 Sinusoidal Functions
角频率
回顾弹簧振荡系统,当阻尼系数b足够小,以致 $b^2-4km<0$时,$m\ddot{x}+b\dot{x}+kx=0$ 的特征方程会有两个复数根(整理为 $-s\pm i\omega_d $ 的形式): $$r=\frac{-b\pm i\sqrt{4mk-b^2}}{2m}=-\frac{b}{2m}\pm i\frac{\sqrt{4mk-b^2}}{2m} $$
这时,ODE的两组基本解(复函数与实函数)为:
$$ [e^{-st}e^{i\omega_d t}, e^{-st}e^{-i\omega_d t}]; \ \ \ [e^{-st}c_1cos(\omega_dt), e^{-st}c_2sin(\omega_dt)] $$
实函数一般解可以表达为:
$$ x(t)=e^{-\frac{b}{2m}t}(c_1cos(\omega_dt)+c_2sin(\omega_dt)) $$
其中,
$$ \omega_d=\sqrt{\frac{4mk-b^2}{4m^2}}=\sqrt{\frac{k}{m}-\frac{b^2}{4m^2}} \ \ \ 即“角频率” $$
这个“角频率”在这里称为阻尼频率。比较这个系统与不带阻尼的系统比较:
$m\ddot{x}+kx=0$,实函数一般解为 $x(t)=c_1cos(\omega t)+c_2sin(\omega t) $ 。这时的角频率 $ \omega_d=\sqrt{\frac{k}{m}} $ , 这时的角频率称为“自然频率”,弹簧自由振荡的情况。
Damped Frequency
在spring-mass-dashpot系统中,当特征方程具有复数根时,微分方程的解将包含一个角频率变量,也称为阻尼频率(damped frequency)。
阻尼频率是指系统存在阻尼的情况下的振荡频率。它是由系统的质量、弹性系数和阻尼系数决定的。当阻尼系数较小时,阻尼频率接近于系统的固有频率(无阻尼情况下的频率)。随着阻尼系数的增加,阻尼频率会逐渐减小,直到达到临界阻尼时,阻尼频率最小。当阻尼系数继续增加时,阻尼频率将变为虚数,整个系统不再振荡。
阻尼频率的存在说明了阻尼对系统振荡的影响。它决定了系统振动的速度和衰减程度。当阻尼较小时,系统会以接近固有频率的频率振动,并且振幅会逐渐衰减。当阻尼较大时,系统的振动频率会降低,并且振幅的衰减速度更快。
在没有阻尼的情况下,spring-mass-dashpot系统的振荡将遵循其固有频率,也称为自然频率(natural frequency)。自然频率是系统在没有外部干扰或阻尼的情况下的固有振动频率。
Angular frequency
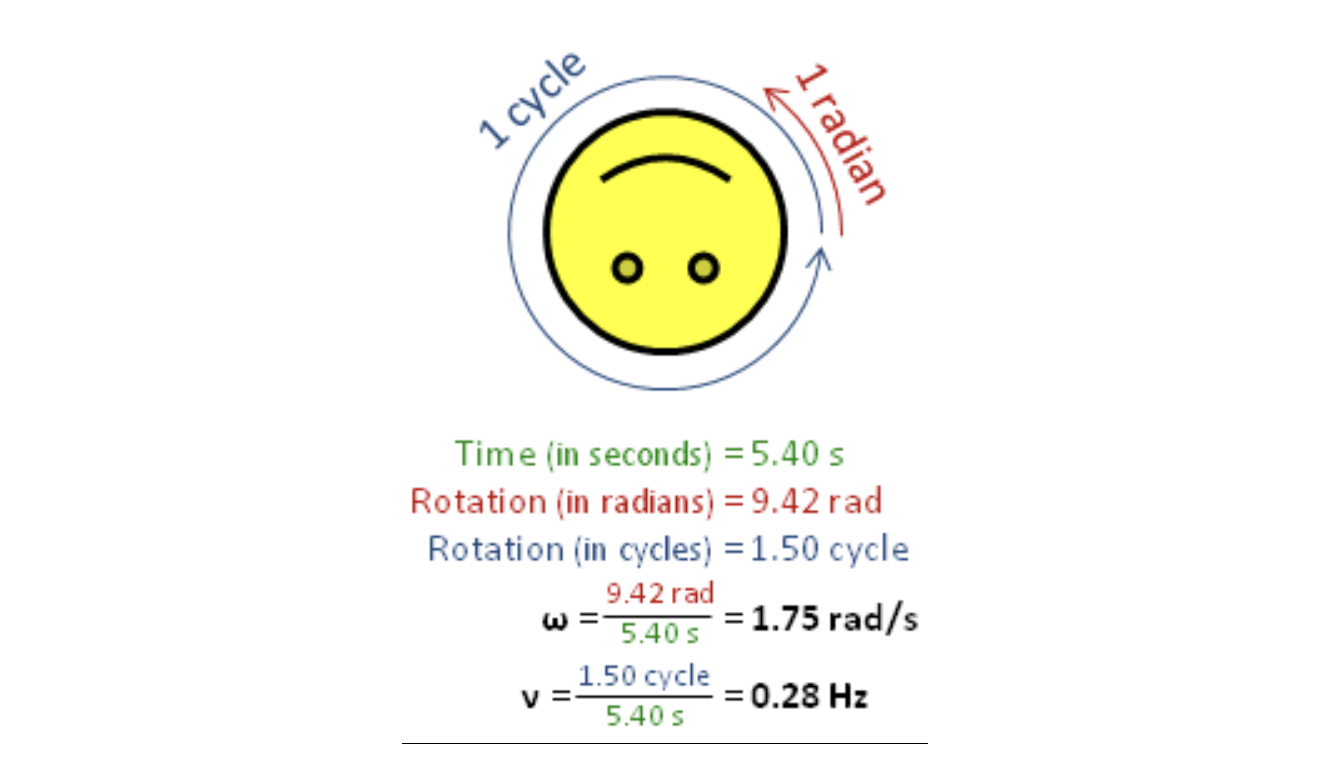
在物理学中,角频率 "ω"(也称为角速度和角率)是每单位时间内角位移的标量度量——每秒旋转多少弧度,也可以看作是正弦函数的参数每秒变化的速度。它决定了振动或波动的周期和频率之间的关系。
振荡系统和波动系统中,角频率与周期和频率之间有一个关系。我们知道,频率是指在单位时间内重复发生的事件的次数。而周期是指一个完整事件循环所需要的时间。这两者之间存在着以下的关系:
频率 = 1 / 周期,即,频率的倒数就是周期。而角频率则表示单位时间内正弦波的相位变化量,也可以看作是正弦函数的参数每秒变化的速度。这个角频率与频率之间的关系是:
角频率 = 2π × 频率
其中,2π是一个常数,代表一个完整的圆周,相当于一个周期。这样,角频率的单位是弧度/秒。
$$ \omega ={\frac {2\pi }{T}}=2\pi f={\frac {v}{r}}={\frac {ds}{dt}}\cdot {\frac {1}{r}}={\frac {d\theta }{dt}} $$
$\square$
正弦函数极坐标式
正弦函数的两种表示形式之间的转换,可以直接通过三角函数和差公式推导出来。在两种形式中所用到的参数之间的关系为:$ A=\sqrt{a^2+b^2} $, $\phi$ 则表示从零点到(a,b)这个点所形成的这条射线与横轴正向所夹的角。点(a,b)作为直角坐标的话,与之相应的,这个的极坐标就是 $(A,\phi)$ 。 $\phi$ 实际上表达了旋转的起点,也就是所谓初始相位。旋转的起点不一定是0弧度,可能是从 $\phi$ 开始。

example
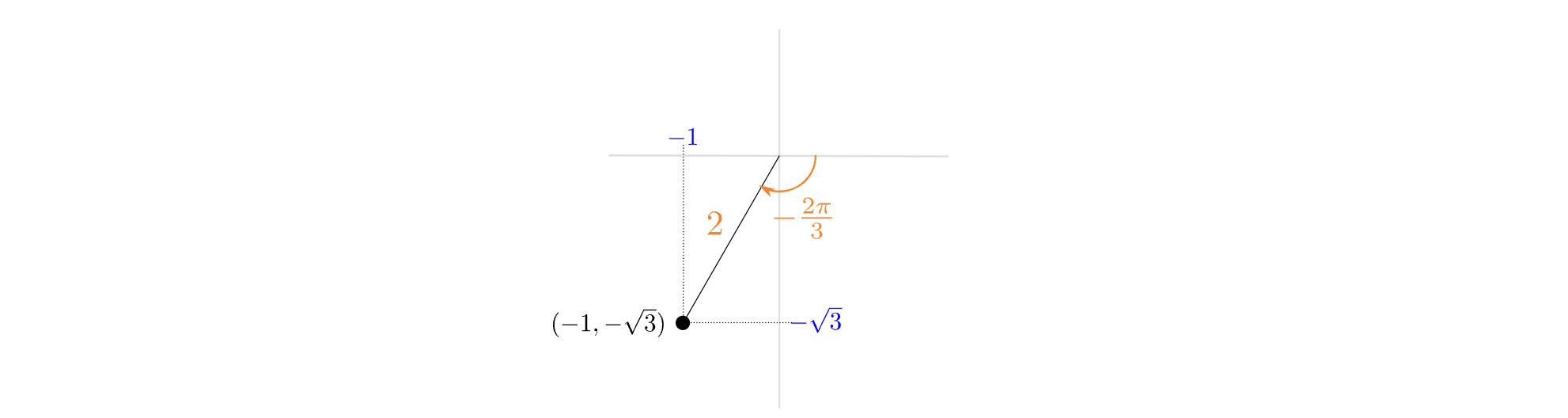
将 $ -cos(5t)-\sqrt{3}sin(5t) $转换到极坐标形式。
这是典型的直接坐标形式,$a=-1, b=-\sqrt{3}$, 因此 A=2(即上图极坐标中的A,相当于r或者模长),角度 $\theta =\omega t=5t$,夹角 $\phi$ 可以通过正切值求得。观察这一直角坐标的特征,可知其在第三象限,因此 primary angle $\phi$ 应为 $-\frac{2\pi}{3}$。所以极坐标形式为:
$ Acos(\omega t-\phi)=2cos(5t+\frac{2\pi}{3}) $
正弦型函数的三种表达式及证明
振幅-相位(极坐标):$Acos(\omega t-\phi)$,这里的常数均为实数;
复数实部:$\large Re(Ce^{i\omega t})$, 这里的C是复数并定义为$ C=a-bi=Ae^{i\theta} $
线性(直角坐标):$ acos\omega t+bsin\omega t $, a和b均为实数。
这三种形式等同,可直接替换。
$$ Re(Ce^{i\omega t})=Acos(\omega t-\phi)=acos\omega t+bsin\omega t $$
$$ C=a-bi=Ae^{i\theta} $$
证明和推导:

example
将$ 7cos(2t-\pi /2) $转换为复数形式 $ Re(Ce^{i\omega t})$.
已经给出$ A=7, \omega=2, \phi=\pi /2 $, 需要找到一个复数C满足 $ \overline{C}=Ae^{i\phi} $, 已知 $\phi$,所以 $\overline{C}=7e^{i\pi /2}=7i $,因此$ C=-7i $。带回原式,$ Re(Ce^{i\omega t})=Re(-7ie^{i2t})$.
example
将 $ -cos(5t)-\sqrt{3}sin(5t) $转换到振幅-相位形式$Acos(\omega t-\phi)$。
和上面转换极坐标是一模一样的题。给出的显然是线性模式$ acos\omega t+bsin\omega t $,因此可以知道$a=-1,b=-\sqrt{3}, \omega = 5 $, 由此可以直接写出对应的复数形式中的a+bi:
$$ Ae^{i\phi}=a+bi=-1-\sqrt{3}i $$
于是,A=2, $\phi=arctan\sqrt{3}=-2\pi /3 $ (第三象限)。 $Acos(\omega t-\phi)=2cos(5t+2\pi /3) $.
构建正弦函数的曲线
从基础正弦波(参考波形)cosx,经过变化(位移、扩张)得到正弦型函数的标准式:
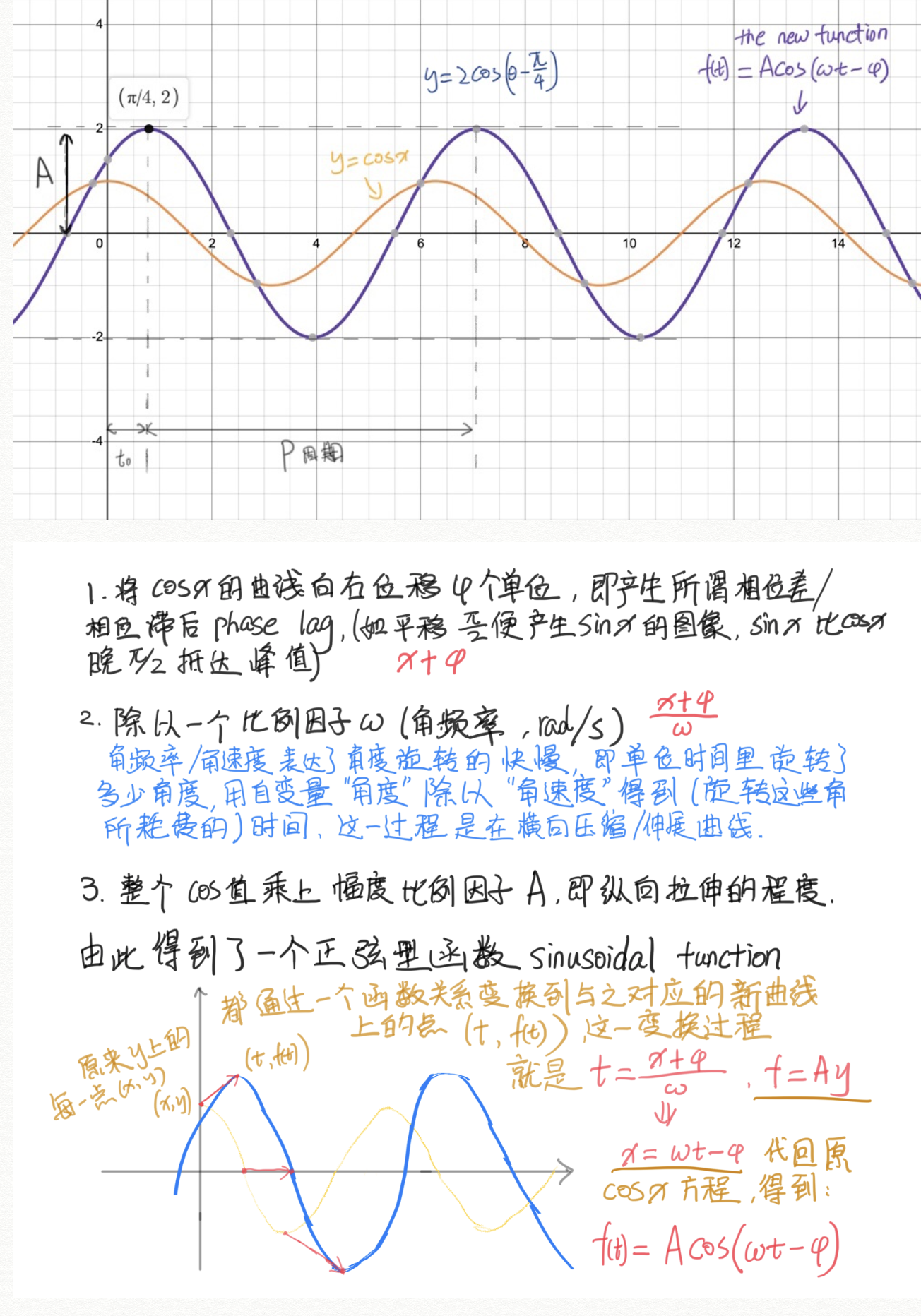
各变量的几何描述及含义
A: 振幅,图像在横轴上方能达到的最大高度;
t_0 (phase lag): 滞后时间,有时记作$\tau$,指初始阶段达到峰值的时间(因为是以标准正弦波作为参考波,即余弦曲线,余弦曲线在t=0是最大值,与它有相位差的曲线,到达峰值就有了一个“滞后”的时间间隔);
P: 周期,完成一个完整振荡的时间,图像上体现为两个相邻的相等极值的距离(or宽度);
t_0 phase lag, P与$\omega,\phi$之间的关联:
$ phase\ lag=\phi / \omega, \ P=2\pi / \omega $
$ (s)=(rad)/(rad/s),\ (s)=(rad)/(rad/s) $
- 直观意义上,$\phi$代表初始阶段的“角度差别”,而除以角速度后,就能得到角度差带来的”时间差“,这正是t_0的定义。
- $P=2\pi / \omega$其实直接表达了周期的含义,试想,在时间上每增加一个P,本质含义就是角度又多旋转了一圈,也就是又往前“行进”了 $2\pi$,除以速度就得到了旋转$2\pi$所用的时间,也就是走完一个周期所用的时间,也就是P本身。
- 由此引申另一个重要的变量关系——频率,频率v是周期P的倒数,所以$\omega=2\pi/P=2\pi v $(有时候用$f$表示); 直观意义上,频率表示单位内完成的周期个数,而一个周期就意味着旋转了一个$2\pi$, 因此频率乘以$2\pi$,就得到了单位时间内旋转的全部角度,而这正是角速度的定义(当然单位是弧度,也属于“无单位”),因此$\omega=2\pi v $。
滞后【相位】与滞后【时间】
$\phi$ 与 $t_0$ phase lag都用来衡量正弦型函数$Acos(\omega t-\phi)$相比于参考波形$cos(\omega t)$ 的偏移程度。但显然t表达的是时间,$\phi$以角度(弧度)来衡量偏移程度,这个初始角度也表达了一个周期的多少【分量】 被偏移了(相比于参考波形)。比如,$\phi=\pi$ 那就意味着偏移了半个周期,这将导致与原参考函数刚好异相,峰值对峰谷。比如 $f(t)=Acos(\omega t-\pi /2) $, 马上就可以知道,是向右移动了1/4个周期。
与之对应的,滞后时间是多少呢?这就得取决于正弦频率了,或者,周期长度。如果它的角频率非常高,那半个周期就会是很短的一点时间。二者之间的转换就取决于角频率:$\large t_0=\phi / \omega $.
按照这种关系,滞后时间也可以很快算出来,因为:
$$ f(t)=Acos(\omega t-\phi)=Acos(\omega (t-t_0)) $$
sinusoidal functions 习题
$$ 考察函数\ \ \frac{e^{i\omega t}}{2+3i} $$
a. 分别写出这个函数极坐标式和直角坐标式下的实部。
【极坐标式】
分子已经是极坐标的形式,分母是标准的复数形式,可以马上计算出$r=\sqrt{13}, tan\phi = 3/2 $,原式可以表示成:
$$ \frac{e^{i\omega t}}{\sqrt{13}e^{i\phi}}=\frac{1}{\sqrt{13}}e^{i(\omega t-\phi)} $$
写成标准的极坐标形式后,可以用欧拉公式马上写出实部的表达式:
$$ Re\lbrace \frac{1}{\sqrt{13}}e^{i(\omega t-\phi)}\rbrace = \frac{1}{\sqrt{13}}cos(\omega t-\phi) $$
其中,$ \phi=arctan(3/2) $
【直角坐标式】
分子可以利用欧拉公式直接改写成cos+isin的形式;分母利用共轭,将虚部cancel掉。
$$ \frac{cos(\omega t)+isin(\omega t)}{2+3i}= \frac{1}{13}(cos(\omega t)+isin(\omega t))(2-3i) $$
将实部分离出来:
$$ \frac{1}{13}(2cos\omega t+3sin\omega t) $$
b. 写出其角频率(circular frequency)、振幅(amplitude)和滞后相位(phase lag)
$$ circ.freq = \omega, \ amp=\frac{1}{\sqrt{13}}, \ phase.lag=\phi=arctan(3/2) $$
ODE习题
[in DE notes Problem 11.9]
找到这个方程的一般解:$ y^{(6)} + 6y^{(5)} + 9y^{(4)} = 0 $
写出特征方程并求解。 $ r^6+6r^5+9r^4=r^4(r^2+6r+9)=r^4(r+3)^2=0 $
方程是6次的,因此有6个根,这个特征方程 r=0, 0, 0, 0, -3, -3. 非全部独立的根也导致原DE的解将够不成完整维度的一般解。$ e^{0t}, e^{0t}, e^{0t}, e^{0t}, e^{-3t}, e^{-3t} $ . 带有重复解的情况(r, r),DE的基本解应为 $ Span(e^{rt}, te^{rt}) $ . 上面六个解替换为:
$$ e^{0t}, te^{0t}, t^2 e^{0t}, t^3 e^{0t}, e^{-3t}, te^{-3t} \ \Rightarrow \ 1, t,t^2,t^3,e^{-3t}, te^{-3t} $$
因此,一般解可以表示为:
$$ c_1+c_2t+c_3t^2+c_4t^3+c_5e^{-3t}+c_6te^{-3t} $$
[in DE notes Problem 11.10]
找到一个最简常系数齐次线性ODE,使得 $ (5t+7)e^{-t}-9e^{2t} $ 是它的一个解。
$ (5t+7)e^{-t}-9e^{2t}=5te^{-t}+7e^{-t}-9e^{2t} $ , 可以看出来,这个解是 $e^{-t},te^{-t},e^{2t}$ 的线性组合,并且可以得知原ODE的特征方程的根一定是-1, -1, 2。因此可以写出特征多项式:$ (r+1)(r+1)(r-2)=r^3-3r-2 $ 。
因此原ODE为:
$$ y^{(3)}-3\dot{y}-2y=0 $$
[in DE notes Problem 11.11]
找到这个方程的实函数基本解:$ y^{3}+3\ddot{y}+9\dot{y}-13y=0 $
首先计算特征方程的根。观察 $r^3+3r^2+9r-13=0 $,1是其中一个根。因此,$(r-1)$ 会是一个因式。运用long division,找到其他因式并计算其他的根。
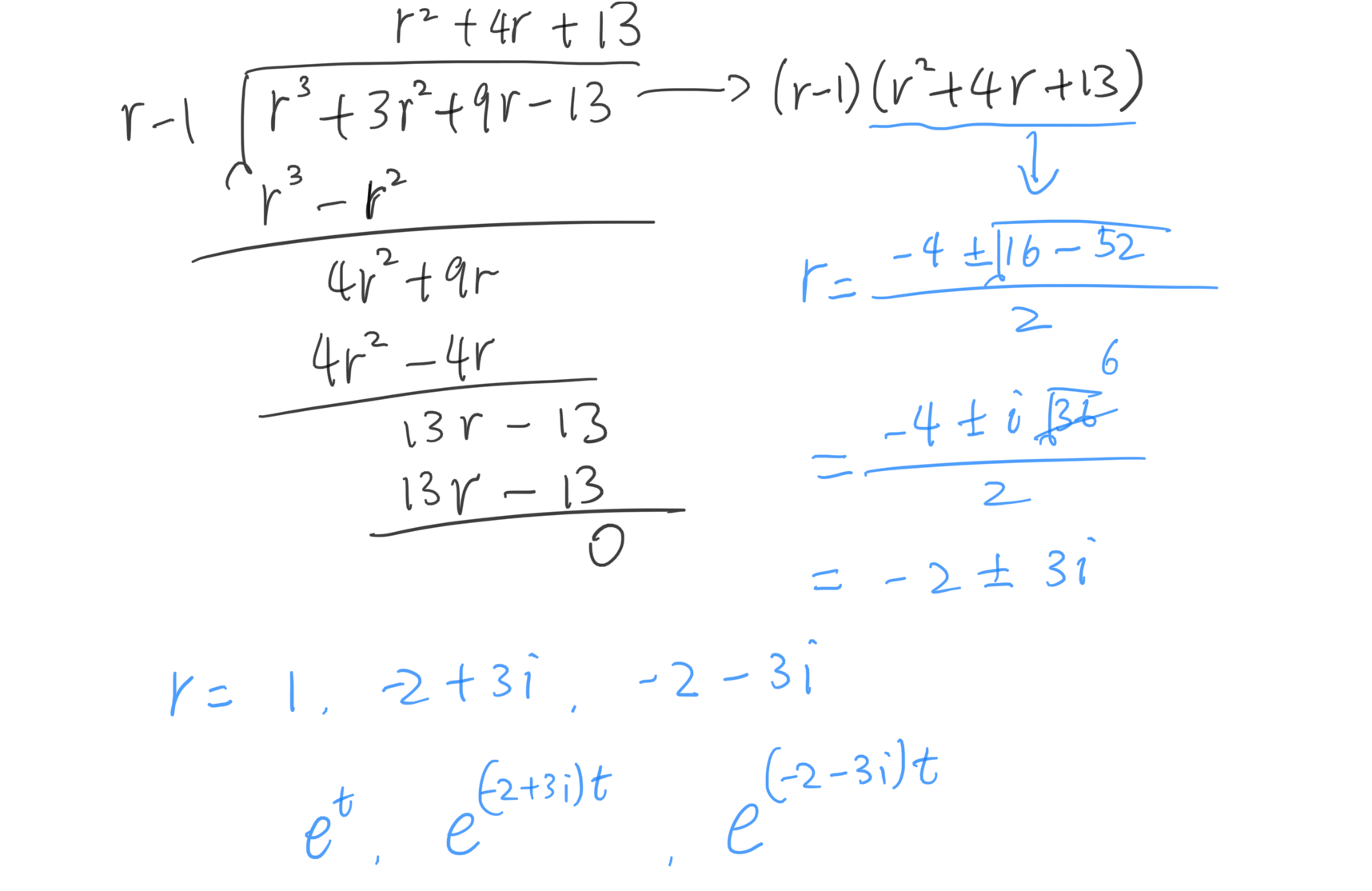
复数根的情况,直接用复数的实部和虚部替代一对共轭复数,得到实函数解:
$$ e^t,e^{-2t}cos(3t),e^{-2t}sin(3t) $$
振荡系统
无阻尼(简谐振荡)
一个质量为1kg的物体被系到弹簧上,弹簧系数为$\pi^2 N/m $, 它被拉到平衡点左侧1米的地方,然后被释放,受到$\pi\ m/s $的向右的力。
$\bullet $ 写出被释放t秒后,物体的位置x(t),使用振幅-相位的形式。默认振幅、角速度均大于零。
根据胡克定律和牛顿第二定律,弹簧的力与其伸长或压缩的距离成正比。力的方向与伸长或压缩的方向相反。根据这个定律,我们可以得到以下微分方程:$ m\ddot{x}=-kx \ \Rightarrow m\ddot{x}+kx=0 $ . 已知 $m=1, k=\pi^2 $ , 所以特征方程为 $ r^2+\pi^2=0 $,得到特征方程的根是 $\pm i\pi $, 因此,实函数解可以写成:$$ x(t)=c_1cos(\pi t)+c_2sin(\pi t) $$
根据题意,$x(0)=-1, \dot{x}(0)=\pi $,有两个初始值就可以计算特解。代入一般解式子中,计算出 $ c_1=-1, c_2=1, x(t)=-cos(\pi t)+sin(\pi t) $ 。
由此可以转换为极坐标形式,$A=\sqrt{2}, tan\phi =-1, \phi = 3\pi /4 $ (第二象限):
$$ x(t)=\sqrt{2}cos(\pi t-\frac{3\pi}{4}) $$
$\bullet $ 写出这个系统的周期P,频率v,滞后时间t_0
$ P=\frac{2\pi}{\omega} \left( \frac{rad}{rad/sec} \right )=2(sec)$. 既然角速度是$\pi$,即每秒钟转半圈,那周期当然就是2秒,因为周期的定义就是转一圈($2\pi$)的时间;
频率是周期的倒数,v=1/2 hertz
“滞后时间”time lag t_0指的是cos(wt)被平移$\phi$所耗费的时间,
$cos(\omega (t-t_0))=cos(\omega t-\phi) \Rightarrow t_0=\frac{\phi}{\omega}=3/4 $.
带阻尼的
带阻尼系统的解与无阻尼系统 (阻尼系数b小到出现复数解) 的解的主要差别是多了一个指数因子:
$$ y=e^{-\frac{b}{2m}t}(c_1cos(\omega_dt)+c_2sin(\omega_dt)) $$
也就是本单元开头部分所写的一般解。把它写成极坐标形式(即振幅-相位形式):
$$ e^{\frac{-b}{2m}t}Acos(\omega_dt-\phi) $$
余弦函数是在1和-1之间振荡,所以y应该在$Ae^{\frac{-b}{2m}t}, \ -Ae^{\frac{-b}{2m}t} $之间振荡。
在unit 2 lecture 5中有一个m=1, b=4, k=5的弹簧阻尼系统,其初始值为$y(0)=1, y'(0)=0$, 其解为$y(t)=e^{-2t}(cost+2sint) $, 现在把它转化为极坐标形式,这一形式可以直观的看到振幅与周期、相位等重要特征。
$ cost+2sint=\sqrt{5}cos(t-\phi), \ tan\phi = 2, \ \phi \approx70^{\circ}$, 因此:
$$ y(t)=\sqrt{5}e^{-2t}cos(t-\phi) $$
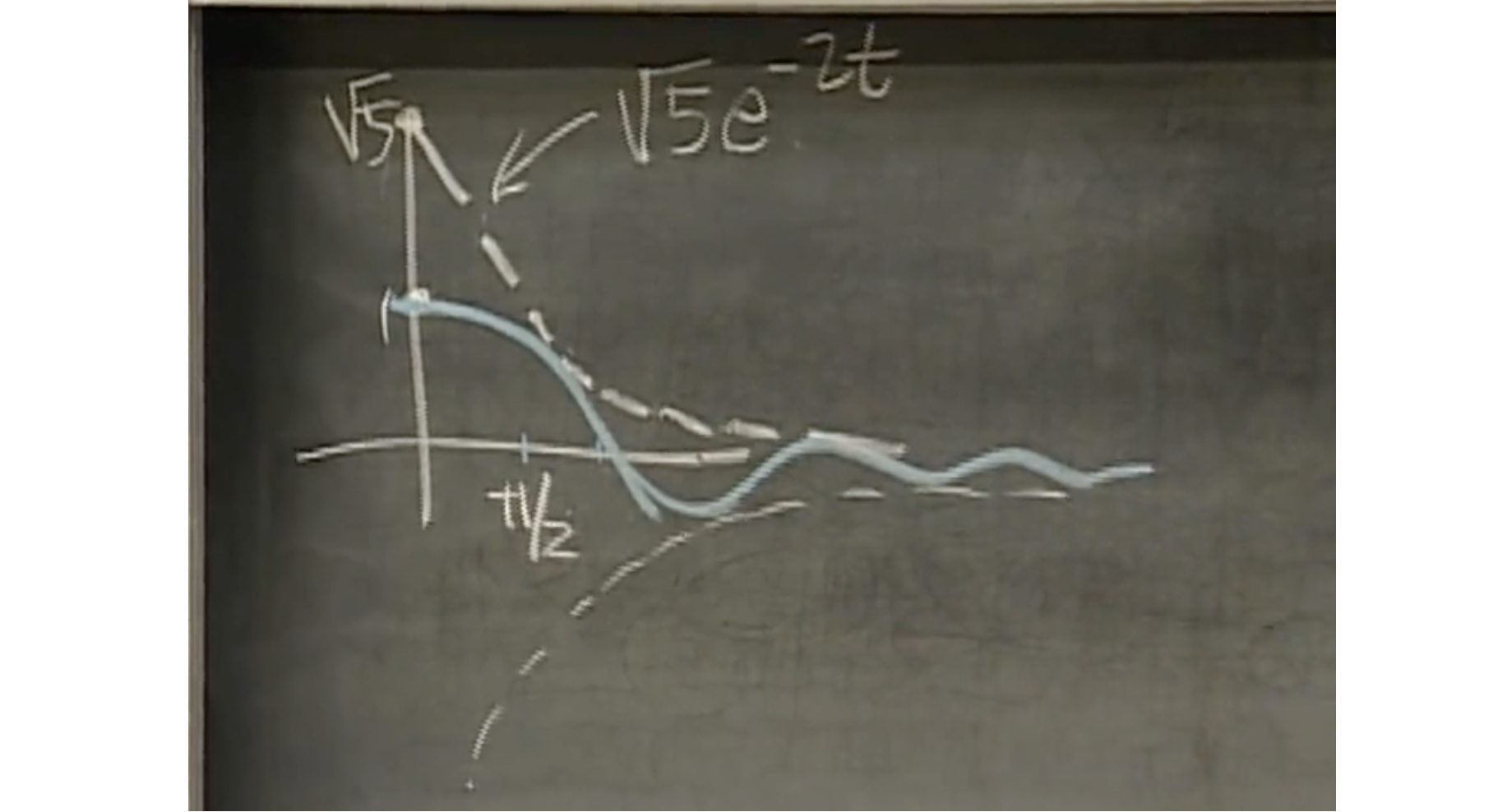
如何解读这个系统?
$\phi$是phase lag,所以这是个稍微滞后一点的余弦函数,最重要的是,它的振幅是在不断下降,$A=\sqrt{5}e^{-2t}$ . 这个曲线的振荡范围就是正负A之间,因此可以用$ \pm\sqrt{5}e^{-2t} $ 两条曲线来预估余弦振荡的大概走势。
sinusoid 应用练习
弹簧-阻尼 练习1
分析这个spring-mass-dashpot系统: m=1, b=2, k=4.
ODE:$ \ddot{x}+2\dot{x}+4x=0 $
特征方程:$ r^2+2r+4=0 $,根:$ -1\pm \sqrt{3}i $
基本解:$ e^{(-1+\sqrt{3}i)t},e^{(-1-\sqrt{3}i)t} $,实解:$ e^{-t}cos\sqrt{3}t,e^{-t}sin\sqrt{3}t $
一般实解:$ e^{-t}(c_1cos\sqrt{3}t+c_2sin\sqrt{3}t) $
阻尼频率:$ \omega_d=\frac{\sqrt{4mk-b^2}}{2m}=\sqrt{3} $
相邻过零点之间的时间间隔:$ 周期=2\pi /\sqrt{3} $,相邻两个过零点为半个周期,因此 $ 时间间隔=\pi /\sqrt{3} $ .
弹簧-阻尼 练习2
1. 振幅-相位模式的特解
物块质量m=1, 弹簧系数k=17/16, 阻尼系数b=1/2, 物块被拉到平衡位置右侧1米,并以一个0.75m/s的向右的速率被释放。求x(t)的振幅-相位表达式。$ x(t)=Ae^{-pt}cos(\omega t-\phi) $
题目给到的已知条件有:$ \ddot{x}+\frac{1}{2}\dot{x}+\frac{17}{16}x=0,\ \ x(0)=1, \dot{x}(0)=0.75 $ .
ODE的特征方程:$ r^2+\frac{1}{2}r+\frac{17}{16}=0 $, 方程有复数根 $ r=-\frac{1}{4}\pm i $ 。因此原DE的一般解为:
$$ e^{-\frac{1}{4}t}(c_1cost+c_2sint) $$
代入初值条件,得到 $ c_1=1, c_2=1 $ . 可得特解:$ e^{-\frac{1}{4}t}(cost+sint) $ ,转化为极坐标形式:$ \sqrt{2}e^{-\frac{1}{4}t}cos(t-\pi/4) $
2. 半衰期half-time
继续上题得到的解。令 $ \epsilon(t)=Ae^{-pt} $,$ \pm \epsilon(t) $ 就表示这个衰减正弦波的振幅函数。“不断衰减”的状态也是区别于纯正弦波的重要特征。 现在计算出振幅减半的时间“半衰期half-time"。
$ t_0=\epsilon(0)=A $,初识振幅也是最大振幅,上题已经得出 $ A=\sqrt{2}$ , 因此,需要计算的时间点就是 $ \epsilon(t)=\sqrt{2}/2 $ 所对应的t值。
$$ \epsilon(t)=\sqrt{2}e^{-\frac{1}{4}t}=\sqrt{2}/2 \ \Rightarrow \ t=ln(16)$$
3. Pseudo-period, pseudo-frequency and time lag
这里的 $\omega=1$, 所以周期等同于纯正弦波 $2\pi$, 频率就是周期的倒数。time lag $t_0=\phi /\omega = \pi/4 $ (利用等式:$ \omega t-\phi=\omega(t-t_0) $ )。
4. 过零点
计算前四个过零点,即 $ x(t)=0$ 的前四个t的值(t>0)。
决定 $ x(t)=0$ 只能是其表达式中的cos的部分。$ cos(t-\pi/4)=0 \ \Rightarrow \ t-\pi/4=\frac{\pi}{2}+k\pi $,k为整数。因此 $ t=\frac{3}{4}\pi+k\pi $, 前四个值就是k=0,1,2,3时的四个值。
7 Damped Harmonic Oscillators 阻尼谐振子
阻尼谐振子
阻尼谐振子,是一个经常在物理学和工程学中讨论的概念。谐振子是指一个具有周期运动的系统,而阻尼则是指该系统受到的能量损耗或减振的过程。
$ \large 回顾总结 $
-
无阻尼情况
$m\ddot{x}+kx=0 , \ p(r)=mr^2+k \ \Rightarrow \text{roots: }\pm \sqrt{-k/m}=\pm i\omega, \omega=\sqrt{k/m} $
基本解:$ e^{i\omega t}, \ e^{-i\omega t}$, 实函数基本解:$ cos(\omega t), sin(\omega t)$ ,
一般解:$ c_1cos(\omega t)+c_2sin(\omega t)$符合这一微分方程的系统称为简谐振荡系统,$\omega$ 称为自然频率。

无阻尼的简谐振荡系统中的自然频率也被称为共振频率(resonant frequency)是因为在此频率下,系统对外部周期性激励呈现出最大的响应。
在一个无阻尼的简谐振荡系统中,当外部激励的频率与系统的自然频率相等时,振动幅度达到最大值。这是因为在自然频率下,激励力与系统的固有振动频率完全同步,能够与系统的振动周期性地增加系统的振幅。
- 带阻尼情况
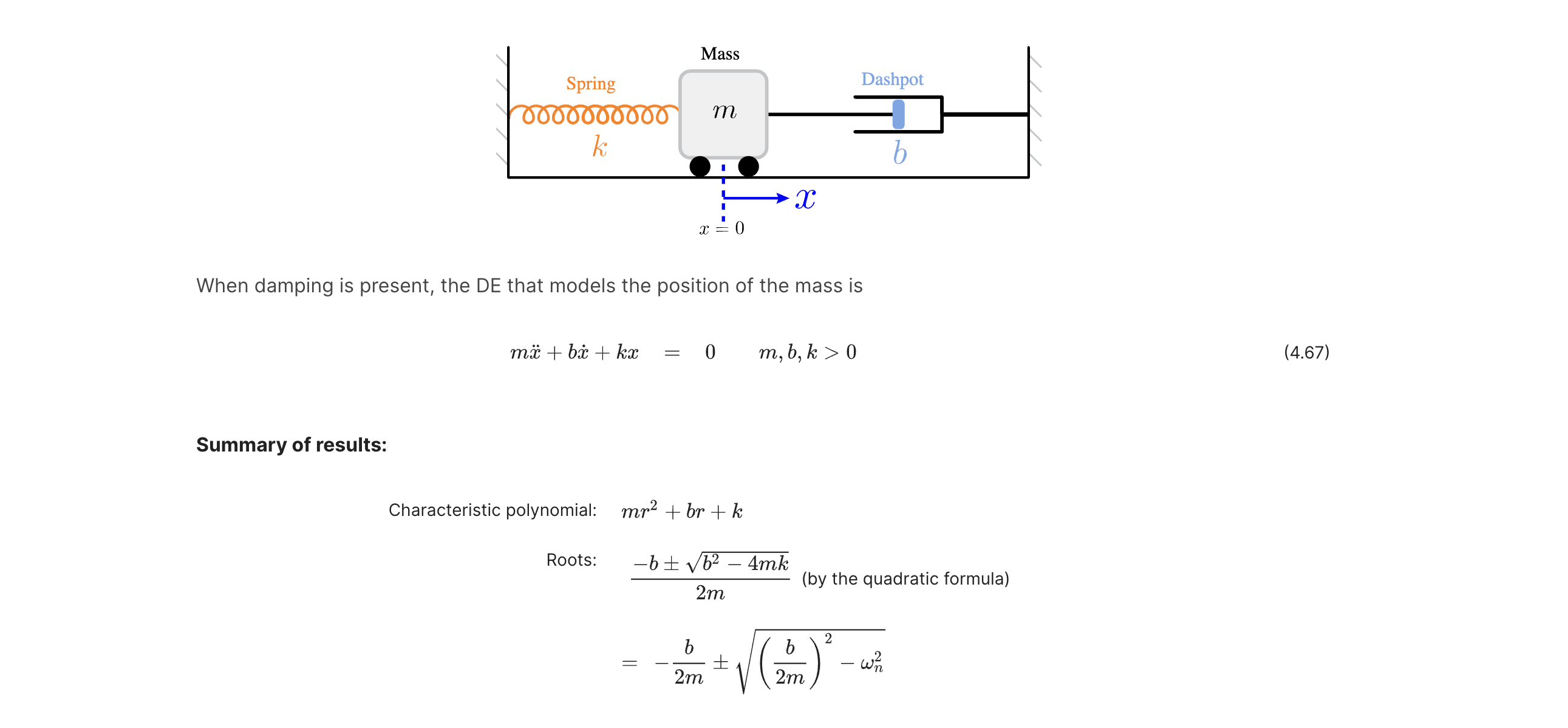
$$ m\ddot{x}+b\dot{x}+kx=0 , \ p(r)=mr^2+k \ \Rightarrow \ \text{roots: }\frac{-b\pm \sqrt{b^2-4mk}}{2m} $$
-
$ b^2<4mk $ :欠阻尼,根为一对共轭复数 $-s\pm i\omega_d,\ s=b/2m$ (positive) ,此时的阻尼频率 $\large \omega_d=\frac{\sqrt{4mk-b^2}}{2m}$ (positive) . 对比上一个自然频率。
基本解:$ e^{(-s+i\omega_d)t}, \ e^{(-s-i\omega_d)t} $ ,实函数基本解:$ e^{-st}cos(\omega_d t), e^{-st}sin(\omega_d t)$
一般解:$\large e^{-st}(c_1cos(\omega_d t)+c_2sin(\omega_d t))$ .
显然,这是一个正弦函数与衰减指数的乘积,其中正弦函数也可以写成“振幅-相位”的形式。所有解具有趋向零的趋势,但不断变换正负号(如上面阻尼题目的图)。欠阻尼系统没有足够量的阻尼使振动彻底消弭。
阻尼系统不仅使的振幅逐渐衰减,频率也变化了,$\omega_d<\omega$ . -
$ b^2=4mk $ :临界阻尼,根为重复的两个实根 $-\frac{b}{2m}, -\frac{b}{2m} $ ,用-s来代表。
基本解:$ e^{-st}, te^{-st} $
一般解:$ \large e^{-st}(c_1+c_2t) $
当 $ t\rightarrow \infty $ 时,$ e^{-st} $ 趋近零,$ te^{-st} $ 也趋近零。临界阻尼情况下,有刚刚好的阻尼使系统的振动消弭。 -
$ b^2>4mk $ :过阻尼,此时的根显然是实数,并且均为负,因为根号下的部分必然小于b。将此时的两个根记为 $ -s_1, -s_2 $,则
一般解:$\large c_1e^{-s_1t}+c_2e^{-s_2t} $
当t趋近于无穷,所有解趋向零。过阻尼系统中,回归平衡点变得缓慢,因为阻尼过大。

比较三种情况下的解的曲线特征:
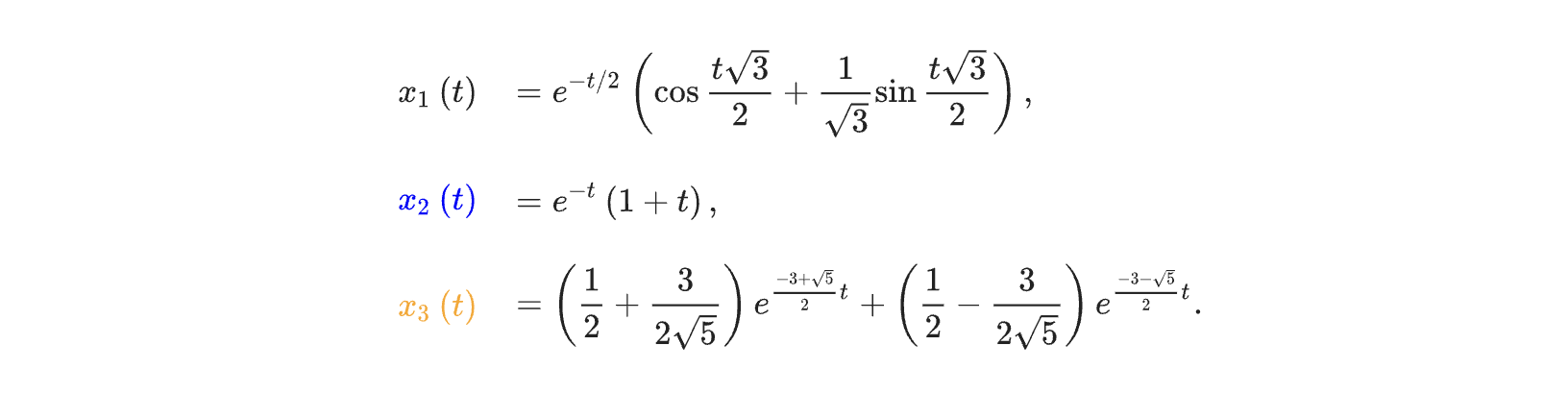
从三个解的形式可以看出x1是某欠阻尼系统的一个解;x2是个临界阻尼系统的一个解;x3是过阻尼系统下的一个解。比较这三个函数的曲线:
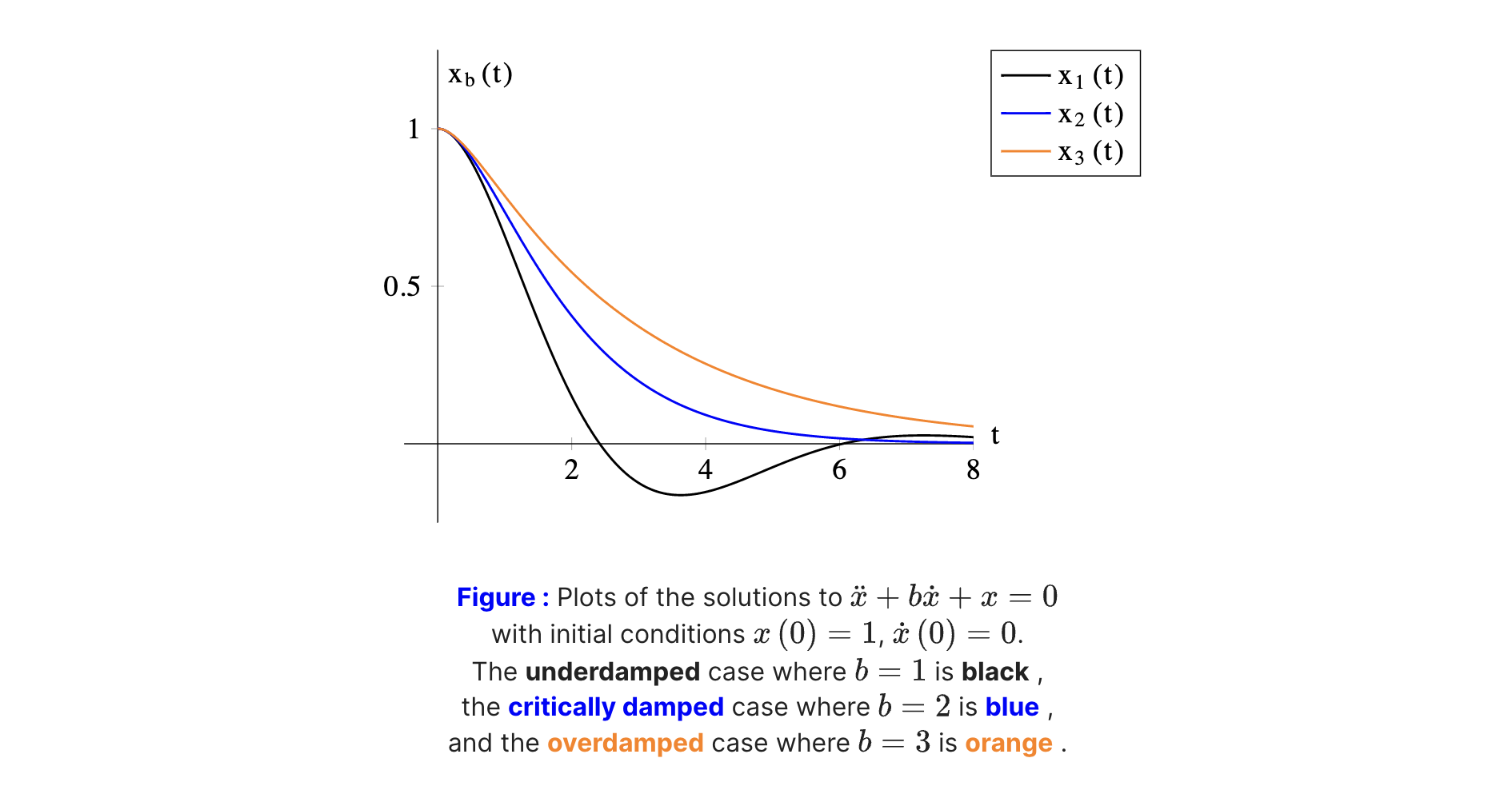
应用题1 船的摇晃
Recitation 7-3: Real life application: the rocking motion of a boat
定义船与水面的角度 $\theta$ , 这里用到了牛顿第二定律,之前用到的都是线性形式 $ ma=m\ddot{x}=F $,但这里需要用到旋转运动的表达形式,物体的转动惯量I(inertia 惯性)乘以物体的⻆加速度,等于作用于物体的力矩τ(torque 扭转力), $ I\ddot{\theta}=\tau $ , 对于指定的船只,I是个常数,τ是关于$\theta$的函数。
视频完整文本及中文翻译
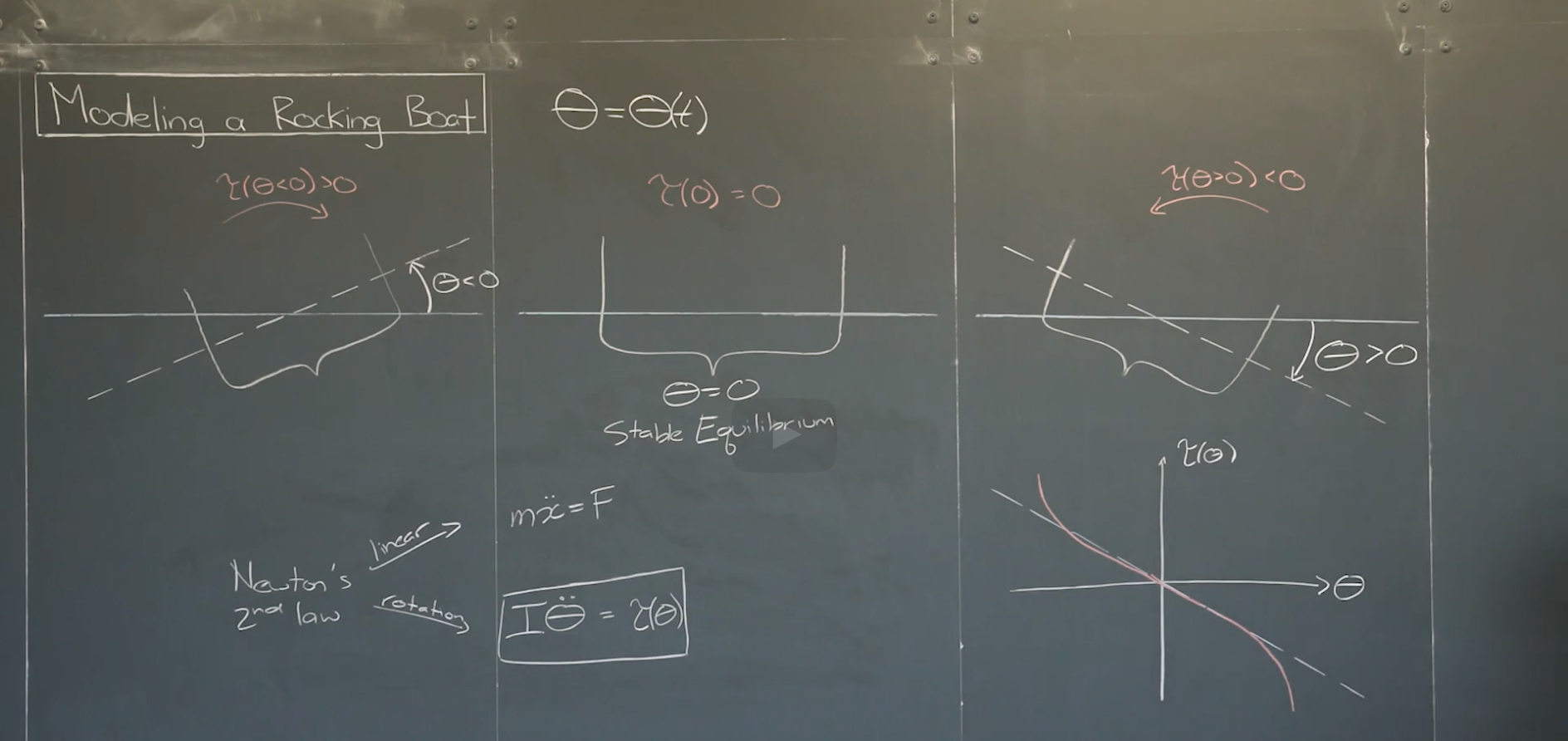
由于只关注很小范围内的旋转情况,这部分接近线性关系,所以取这段曲线原点部分的切线,作为近似的线性表达,-k是它的斜率。$ I\ddot{\theta}=\tau \sim -k\theta, \ \text{where k>0,}\ \theta \ll 1 $
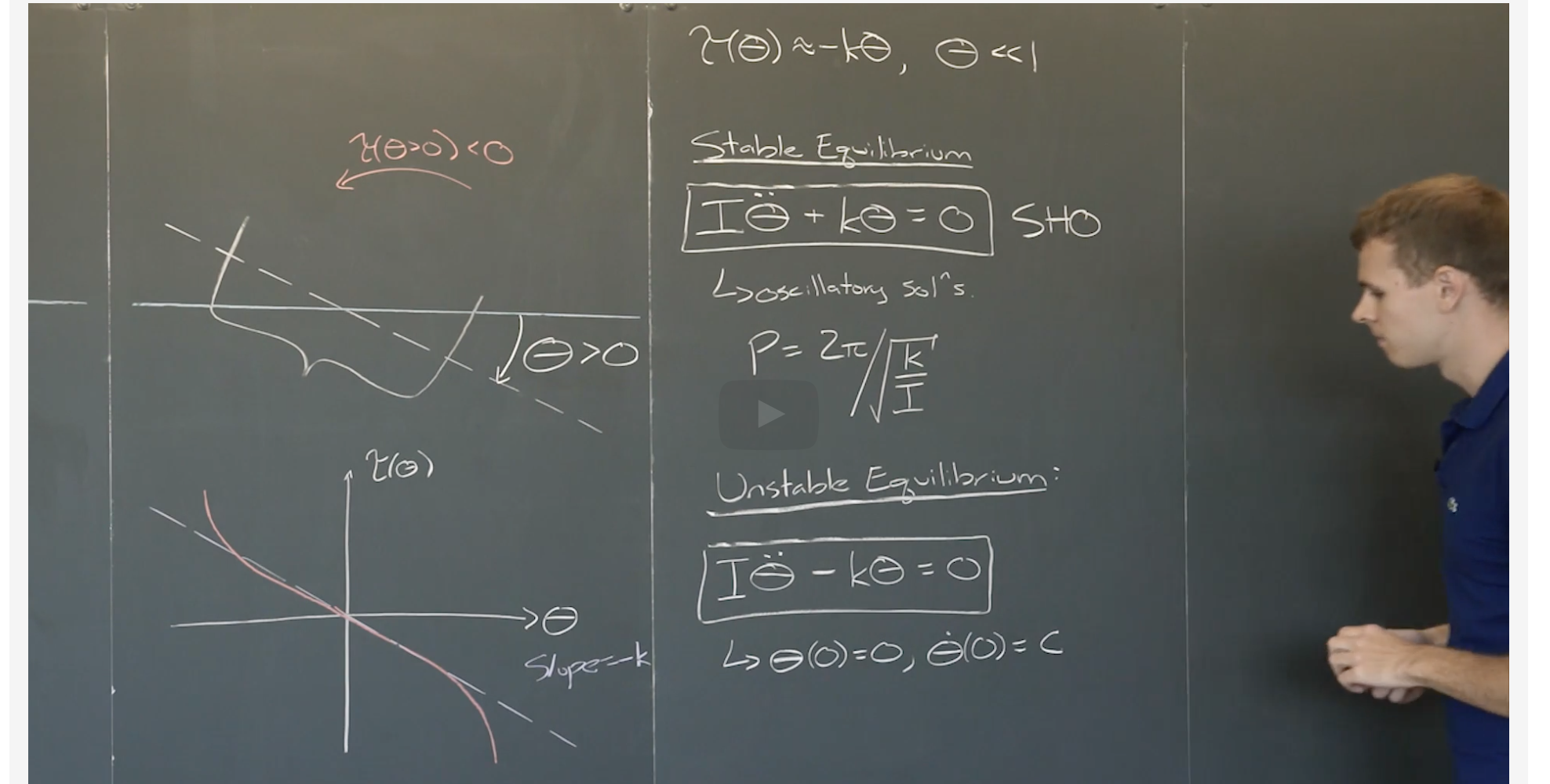
将得到的τ的表达式,代回前面牛顿第二定律式子中,得到具有稳定平衡的船只运动的DE表达式:$ I\ddot{\theta}+k\theta=0 $ ,这个形式显然是简谐振荡的DE。我们知道周期 $ P=2\pi / \omega = 2\pi / \sqrt{\frac{k}{I}} $ 。这里把船的晃动视为简谐振荡,省略了阻尼项,船的实际运动振幅是在不断减小的,实际上应该有阻尼项。这里简化了,不过对于很小阶段内的摆动,目前这个式子已经足够表达船的运动。
但是不同形状的船并不一定总有稳定平衡。此时的斜率为正,DE表示为 $ I\ddot{\theta}-k\theta=0 $ ,给出初值,$ \theta(0)=0, \dot{\theta}(0)=c $ ,求这种情况下的特解(用k,I,c表示)。
$ \theta(t)=\frac{c}{2} \sqrt{I/k}\cdot e^{\sqrt{k/I}\cdot t}-\frac{c}{2} \sqrt{I/k}\cdot e^{-\sqrt{k/I}\cdot t} $
在不稳定平衡的情况下,平衡点附近的力矩会有一个正斜率,是因为当船只略微偏离平衡位置时,它会受到一个迎头方向的恢复力矩。这个正斜率意味着随着船只的偏离越来越大,恢复力矩也会越来越强,试图把船只推回平衡位置。
举个例子,假设我们将一个球放在山坡上。如果山坡曲线在球的平衡点附近朝下倾斜,球一旦离开平衡位置,重力就会使得球下滚,带来一个与偏离方向相反的恢复力矩。这个恢复力矩对应于力矩函数在平衡点附近有一个负斜率。
然而,如果山坡曲线在球的平衡点附近朝上倾斜,球一旦离开平衡位置,重力将推动球向下滚动,而这个恢复力矩将与偏离方向相同,试图使球继续远离平衡位置。这个情况下的恢复力矩对应于力矩函数在平衡点附近有一个正斜率。
因此,在不稳定平衡的情况下,力矩函数的斜率为正,表示了力矩的方向与偏离方向相同,试图进一步推动系统脱离平衡。这样的不稳定平衡将导致船只在进入水中时倾斜到一侧,增加倾覆的风险。
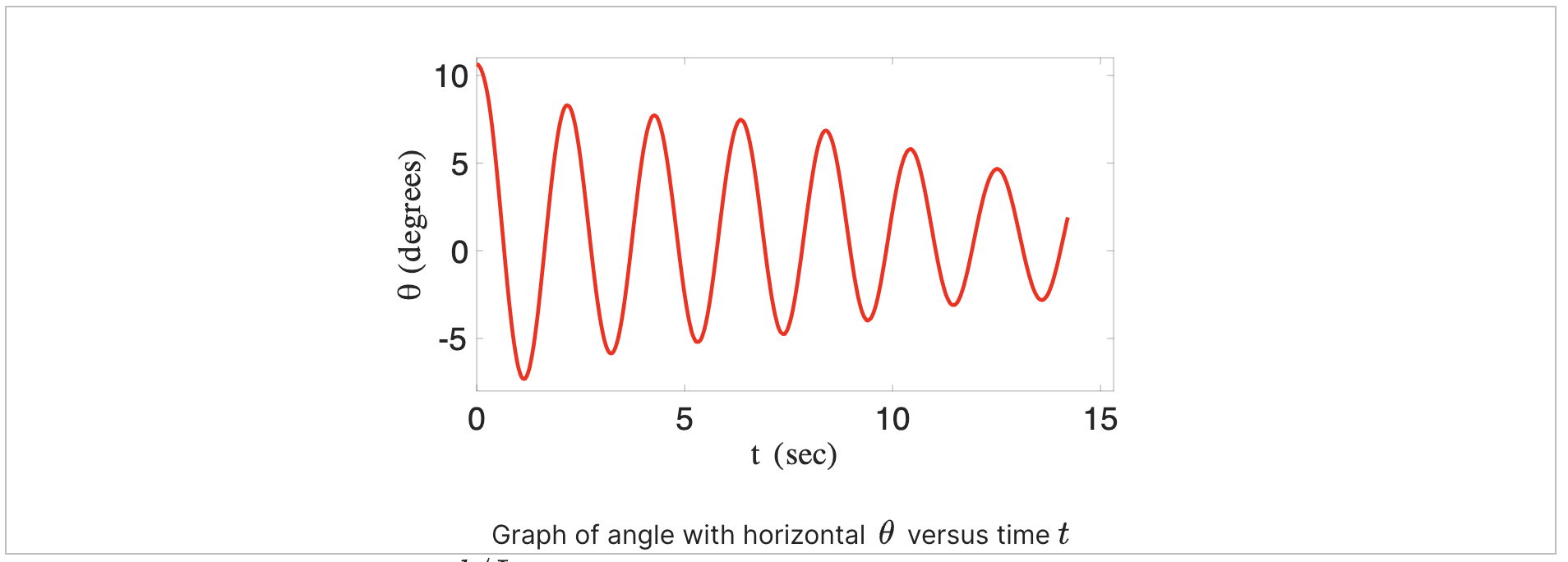
用这个图表估算k/I的比值。
周期P约为2,由于 $ P=2\pi/\omega=2 $ ,可知 $ \pi=\omega $ 。之前的无阻尼系统中已经总结过,自然频率 $ \omega=\sqrt{k/m}=\sqrt{k/I} $ ,由此可知, $ k/I=\pi^2 $ 。
