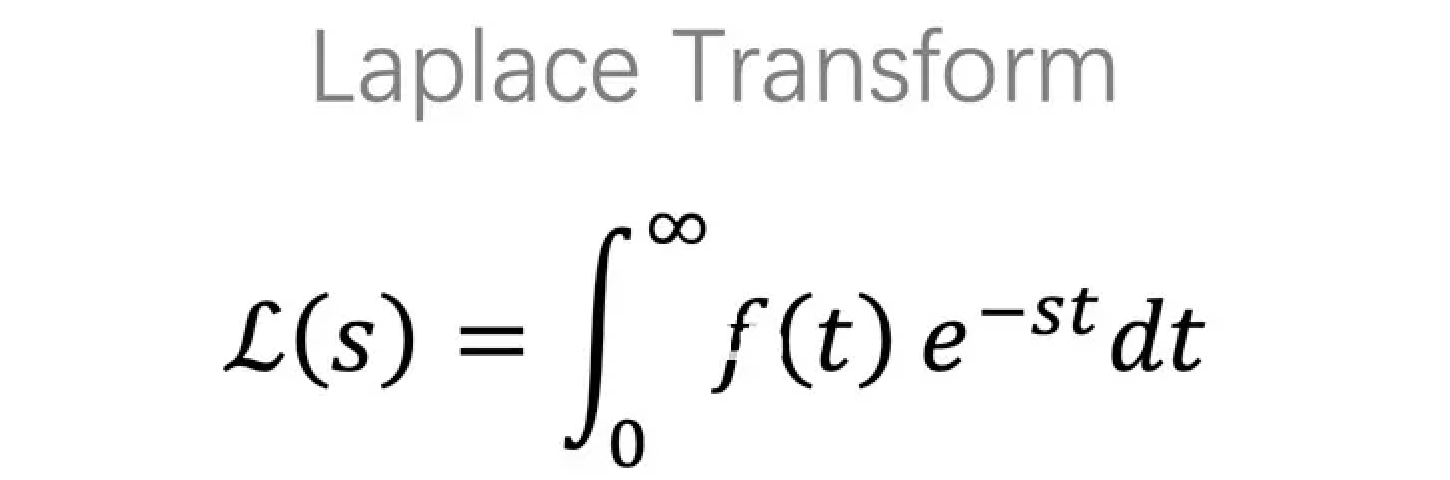
Part I - A first glance
the first step into Laplace transform
Transform is like a function of function, a function takes one set of numbers to another set of numbers, and the trnsform takes one set of functions to another set of functions.
$ \mathscr{L} \lbrace f(t)\rbrace \longrightarrow F(s) $
$$ \mathscr{L} \lbrace f(t) \rbrace=\int^{\infty}_0 e^{-st}f(t) dt $$
L{1}
举例一个非常简单的函数 $ f(t)=1$ , assume $ s>0$ .
$$ \mathscr{L} \lbrace 1\rbrace=\int^{\infty}0 e^{-st}dt = \lim\limits{A\to\infty}\int^{A}0 e^{-st}dt=\lim\limits{A\to\infty} \left[-\frac{1}{s}e^{-st} \right]0 ^{A}=\lim\limits{A\to\infty} \left( -\frac{1}{s}e^{-sA}+\frac{1}{s} \right)=\frac{1}{s} $$
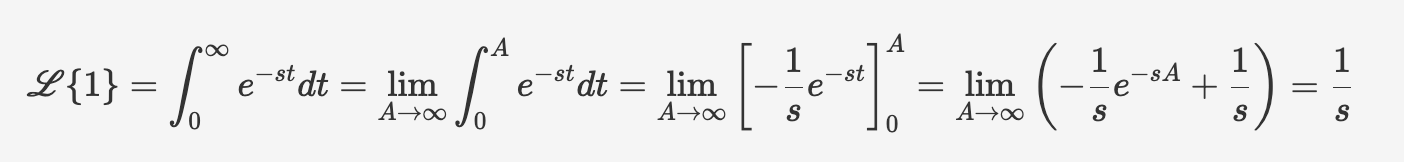
so we got our first Laplace transform $ \mathscr{L} \lbrace 1\rbrace=\frac{1}{s} $ .
L{e^at}
$$ \mathscr{L} \lbrace e^{at} \rbrace= \int^{\infty}_0 e^{-st}e^{at}dt=\int^{\infty}_0 e^{(a-s)t}dt=\frac{1}{a-s} \left[e^{(a-s)t} \right]_0 ^{\infty} $$
if $a-s>0 $, there's no limit and the Laplace transform will be undefined; $$ \mathscr{L} \lbrace \sin at \rbrace= \int^{\infty}_0 e^{-st}\sin at \ dt $$
if $a-s<0 $: $ \frac{1}{a-s} \left[e^{(a-s)t} \right]_0 ^{\infty}=\frac{1}{a-s}(0-1)=\frac{1}{s-a} $ .
Therefore, $ \mathscr{L} \lbrace e^{at} \rbrace=\frac{1}{s-a}, \ (aL{sin(at)}
so the Laplace transform is: $$ \mathscr{L} \lbrace \sin at \rbrace=\frac{a}{s^2+a^2} $$
properties of the Laplace transform
$$ \mathscr{L} \lbrace c_1f(t)+c_2g(t) \rbrace=c_1\mathscr{L} \lbrace f(t) \rbrace+c_2\mathscr{L} \lbrace g(t) \rbrace $$
Why the Laplace transform is extremely useful in soloving differential equations?
L{f'(t)}
consider $ f'(t) $'s Laplace transform.
$ \mathscr{L} \lbrace f'(t) \rbrace=\int^{\infty}_0 e^{-st}f'(t) $ ,

Therefore,
$$ \large \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) $$
按照这个规律,能够得出更高阶导函数的Laplace变换。
$ \mathscr{L} \lbrace f''(t) \rbrace=s\mathscr{L} \lbrace f'(t) \rbrace-f'(0)\ \ \ \ \lceil \text{plug in}\ \mathscr{L} \lbrace f'(t) \rbrace\rfloor $
$ =s \left(s\mathscr{L} \lbrace f(t) \rbrace-f(0) \right)-f'(0) $
$ =s^2\mathscr{L} \lbrace f(t) \rbrace-sf(0)-f'(0) $
$ \mathscr{L} \lbrace f'''(t) \rbrace=s\mathscr{L} \lbrace f''(t) \rbrace-f''(0)\ \ \ \ \lceil \text{plug in}\ \mathscr{L} \lbrace f''(t) \rbrace\rfloor$
$ =\mathscr{L} \lbrace f'''(t) \rbrace=s\left(s^2\mathscr{L} \lbrace f(t) \rbrace-sf(0)-f'(0) \right)-f''(0)$
$ =s^3\mathscr{L} \lbrace f(t) \rbrace-s^2f(0)-sf'(0)-f''(0)$
观察:
$\large \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) $
$\large \mathscr{L} \lbrace f''(t) \rbrace=s^2\mathscr{L} \lbrace f(t) \rbrace-sf(0)-f'(0) $
$\large \mathscr{L} \lbrace f'''(t) \rbrace=s^3\mathscr{L} \lbrace f(t) \rbrace-s^2f(0)-sf'(0)-f''(0) $
$\large \mathscr{L} \lbrace f^{4}(t) \rbrace=s^4\mathscr{L} \lbrace f(t) \rbrace-s^3f(0)-s^2f'(0)-sf''(0)-f'''(0) $
......
L{cos(at)}
利用
$ \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) $ 和
$ \mathscr{L} \lbrace \sin at \rbrace=\frac{a}{s^2+a^2} $
找到cos(at)的Laplace变换 $ \mathscr{L} \lbrace \cos at \rbrace $。
Assume cos(at) is the derivate of some function, what's the function then?
if $ f'(t)=\cos at $ , what's the potential f(t)? $\large f(t)=\frac{1}{a}\sin at $ .
$$ \mathscr{L} \lbrace \cos at \rbrace=s\mathscr{L} \lbrace \frac{1}{a} \sin at \rbrace-\frac{1}{a}\sin 0= \frac{s}{a}\mathscr{L} \lbrace \sin at \rbrace=\frac{s}{a} \frac{a}{s^2+a^2}=\frac{s}{s^2+a^2} $$
Therefore,
$$ \large \mathscr{L} \lbrace \sin at \rbrace = \frac{a}{s^2+a^2} $$
$$ \large \mathscr{L} \lbrace \cos at \rbrace = \frac{s}{s^2+a^2} $$
L{polynomial}
利用 $\mathscr{L}\lbrace 1\rbrace=\frac{1}{s} $ 和 $ \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) $ 求更多函数。
$$ \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) \ \Rightarrow \ \mathscr{L} \lbrace f(t) \rbrace=\frac{1}{s} [\mathscr{L} \lbrace f'(t) \rbrace+f(0)] $$
there's a function $f(t)=t$ ,use the equation above to find its Laplace transformation.
$ \mathscr{L} \lbrace t\rbrace=\frac{1}{s} [\mathscr{L}\lbrace 1\rbrace + f(0)]=$ $\Large\frac{1}{s^2} $
根据基本定义,$ \mathscr{L} \lbrace t\rbrace=\int^{\infty}_0 e^{-st}t\ dt$ ,因此可以利用逆向的product rule来求解,但是利用上述规律要简易的多。
再求 $ \mathscr{L} \lbrace t^2\rbrace=\frac{1}{s} [\mathscr{L}\lbrace 2t\rbrace + f(0)]=\frac{2}{s}\mathscr{L} \lbrace t\rbrace=\frac{2}{s} \frac{1}{s^2} =$ $\Large\frac{2}{s^3} $
再求 $ \mathscr{L} \lbrace t^3\rbrace=\frac{1}{s} [\mathscr{L}\lbrace 3t^2\rbrace+f(0)]=\frac{3}{s}\mathscr{L} \lbrace t^2\rbrace=\frac{3}{s} \frac{2}{s^3}=$ $\Large\frac{3\cdot 2}{s^4} $
in general,
$$ \large \mathscr{L} \lbrace t^n\rbrace=\frac{n!}{s^{n+1}} $$
$\clubsuit$ 用基本定义推导这个等式:

"shifting" the transform
shifting transform by multiplying function by exponential
尝试另一个角度看待变换后的函数。
从函数本身的基本性质出发,回忆函数中变换自变量的情形。
某个函数,如果被乘上一个指数函数再做拉普拉斯变换:
$ \mathscr{L} \lbrace e^{at}f(t) \rbrace= \int^{\infty}_0 e^{-st}e^{at}f(t)\ dt=\int^{\infty}_0 e^{(a-s)t}f(t) \ dt$
观察 $ \mathscr{L} \lbrace e^{at}f(t) \rbrace$ 与 $ \mathscr{L} \lbrace f(t) \rbrace $,二者区别在哪?
$$ \mathscr{L} \lbrace f(t) \rbrace\ =\ \int^{\infty}_0 \ e^{-st}f(t) \ dt \ \ \longrightarrow \ \mathscr{L} \lbrace e^{at}f(t) \rbrace=\int^{\infty}_0 e^{(a-s)t}f(t) \ dt $$
如果把变换后的结果看作关于s的函数 $\mathscr{L} \lbrace f(t) \rbrace=F(s)$,以上两个结果等同于函数的自变量s进行了平移变化,s变成了s-a, a-s=-(s-a),函数仍为F 。 因此,
$$ 如果\ \mathscr{L} \lbrace f(t) \rbrace=F(s),那么\ \mathscr{L} \lbrace e^{at}f(t) \rbrace=F(s-a) $$
对任意函数乘以指数函数后,对Laplace变换的影响就如此。要注意,F(s)这个函数指的是什么。回忆傅里叶变换,一个关于某变量的函数后来变成了关于其他变量的函数,这里也是如此。transform指的正是关于某自变量的函数被“变换”成了关于别的自变量的函数。
前面已经计算过,$ \mathscr{L} \lbrace \cos at \rbrace=\large \frac{s}{s^2+a^2} $,如果设定 $ \mathscr{L} \lbrace \cos 2t \rbrace=F(s)=\large \frac{s}{s^2+4}$ , 那么 $ \mathscr{L} \lbrace e^{3t} cos2t \rbrace=?$
按照如上规律,这个 $\mathscr{L} \lbrace e^{3t} cos2t \rbrace=F(s-3)$
如果 $F(s)=\frac{s}{s^2+4} \ \Rightarrow \ F(s-3)=\large \frac{s-3}{(s-3)^2+4}$ ,把s替换成s-3即可。
unit step function 单位跃阶函数 Heaviside step function
关于单位跃阶函数的Laplace变换
首先构建单位跃阶函数:
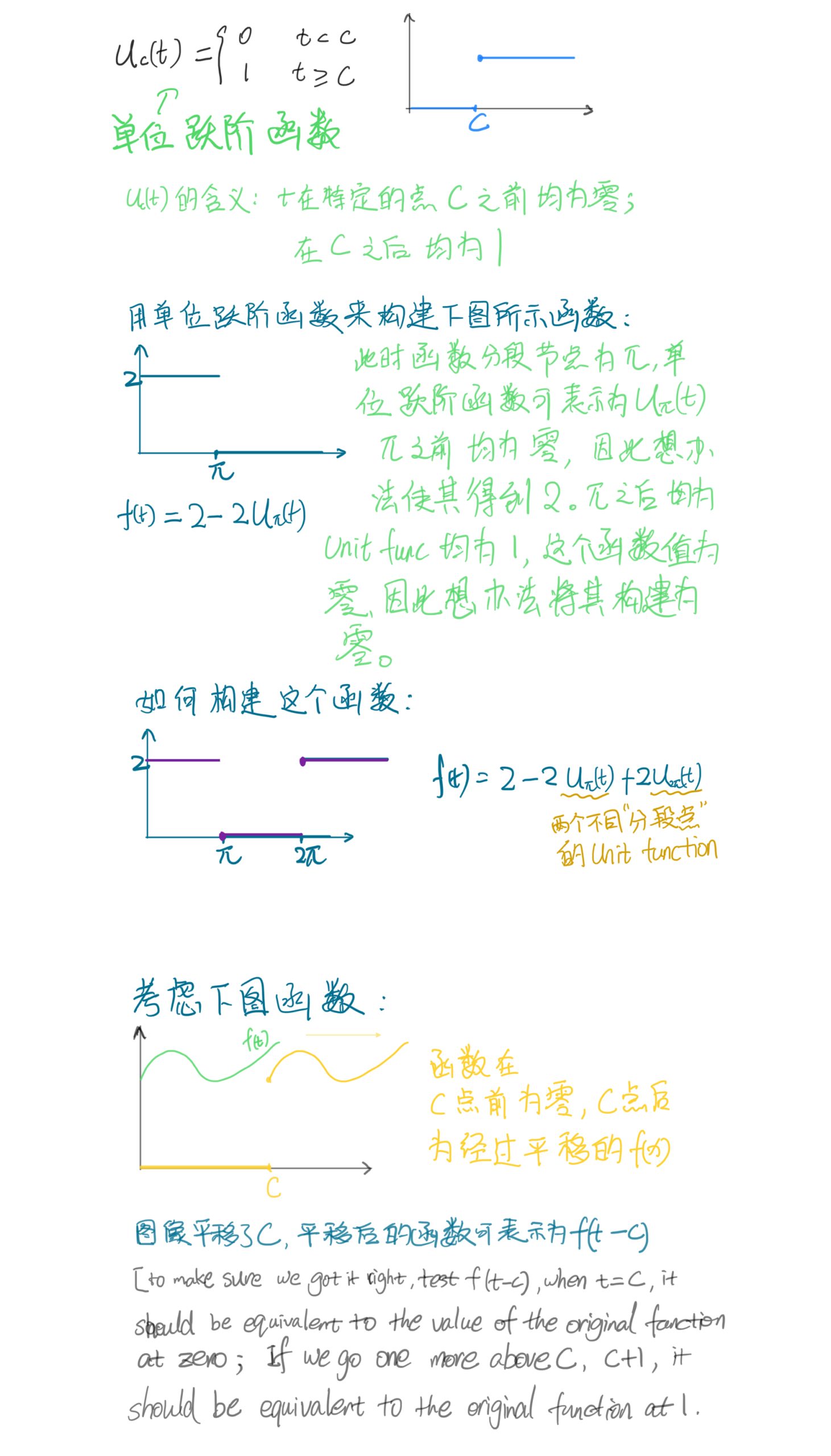
考察构建后的函数的Laplace变换
$ \mathscr{L} \lbrace \ u_c(t)f(t-c) \rbrace=\int^{\infty}_0 e^{-st}u_c(t)f(t-c)\ dt $

因此得到,
$$ \mathscr{L} \lbrace \ u_c(t)f(t-c) \rbrace=e^{-sc} \mathscr{L} \lbrace f(t) \rbrace=e^{-sc} F(s) $$
Part II Laplace Transform and More
quick review
基本定义:
$$ \mathscr{L} \lbrace f(t) \rbrace =\int^{\infty}_0 e^{-st}f(t) \ dt =F(s) $$
与单位跃阶函数相乘:
$$ \mathscr{L} \lbrace u_c(t)f(t-c) \rbrace= e^{-cs}F(s) $$
与指数函数相乘:
$$ \mathscr{L} \lbrace e^{at}f(t) \rbrace=F(s-a) $$
基础函数的Laplace变换:
$$ \mathscr{L} \lbrace 1 \rbrace=\frac{1}{s} $$
$$ \mathscr{L} \lbrace e^{at} \rbrace= \frac{1}{s-a} $$
$$ \mathscr{L} \lbrace t^n \rbrace=\frac{n!}{s^{n+1}} $$
$$ \mathscr{L} \lbrace \sin at \rbrace=\frac{a}{s^2+a^2} $$
$$ \mathscr{L} \lbrace \cos at \rbrace=\frac{s}{s^2+a^2} $$
[========]
Inverse Laplace
consider some function's Laplace transform is this:
$ F(s)=\frac{3!}{(s-2)^4} $,observe the pattern, try this:
$$ \mathscr{L} \lbrace t^3 \rbrace=\frac{3!}{s^{4}} $$
the target transform is a shifting of the above one, so try this:
$$ \mathscr{L} \lbrace e^{2t}f(t) \rbrace=F(s-2) $$
therefore, the original function is $\large e^{2t}t^3 $ .
EXAMPLE
consider the inverse Laplace transform of
$$ F(s)=\frac{2(s-1)e^{-2s}}{s^2-2s+2} $$

therefore,
$$ \mathscr{L}^{-1} \left\lbrace \frac{2(s-1)e^{-2s}}{s^2-2s+2} \right\rbrace =2u_2(t)e^{t-2}cos(t-2) $$
[========]
Dirac delta function
definition of Dirac function
we define Dirac function
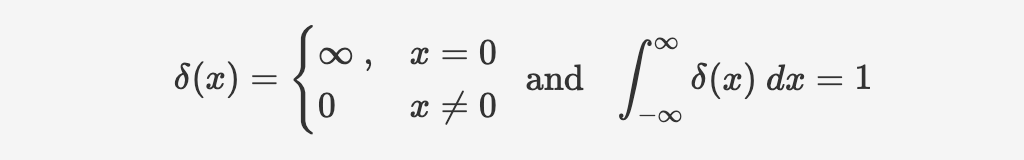
validation of Dirac function
To understand the integral which is 1, consider a step function:

if we take the integral of it:
$\int_{-\infty} ^{\infty} \delta(\tau) \ dt $ ,be careful of that $\tau$ is a constant and the variant is t.
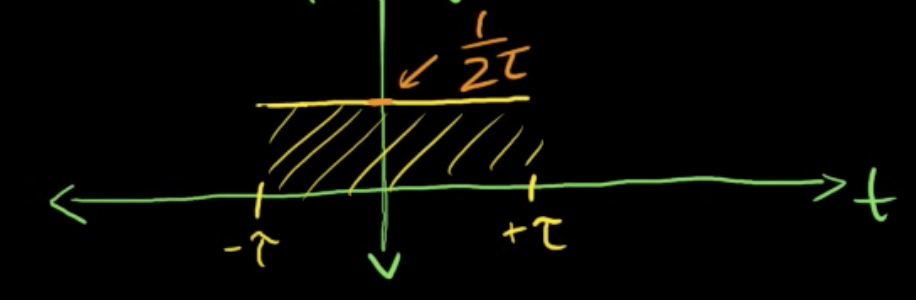
There is some area only between $ -\tau\ and \ \tau $ , so the integral is equal to $\int_{-\tau} ^{\tau} \frac{1}{2\tau} \ dt $ .
it's a square apparently, so the area is the base ($2\tau$) times the height ($\frac{1}{2\tau}$) which is 1. Therefore we got:
$$ \int_{-\infty} ^{\infty} \delta(\tau) \ dt=1 $$
To validate it, calculate the integration,
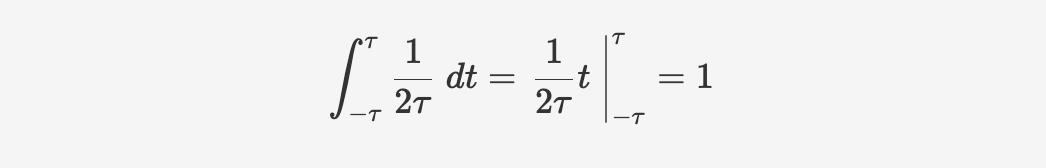
If we take smaller and smaller $\tau$, which means the boundary is going infinitly toward zero, it'll eventually become the Diract function:
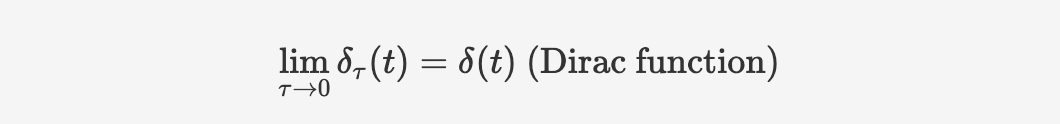
And the limit of the integral of the step function $\delta _\tau(t)$ will be one:
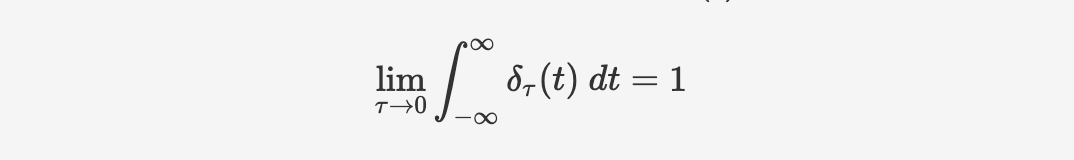
Therefore, the integration of Dirac function is 1.
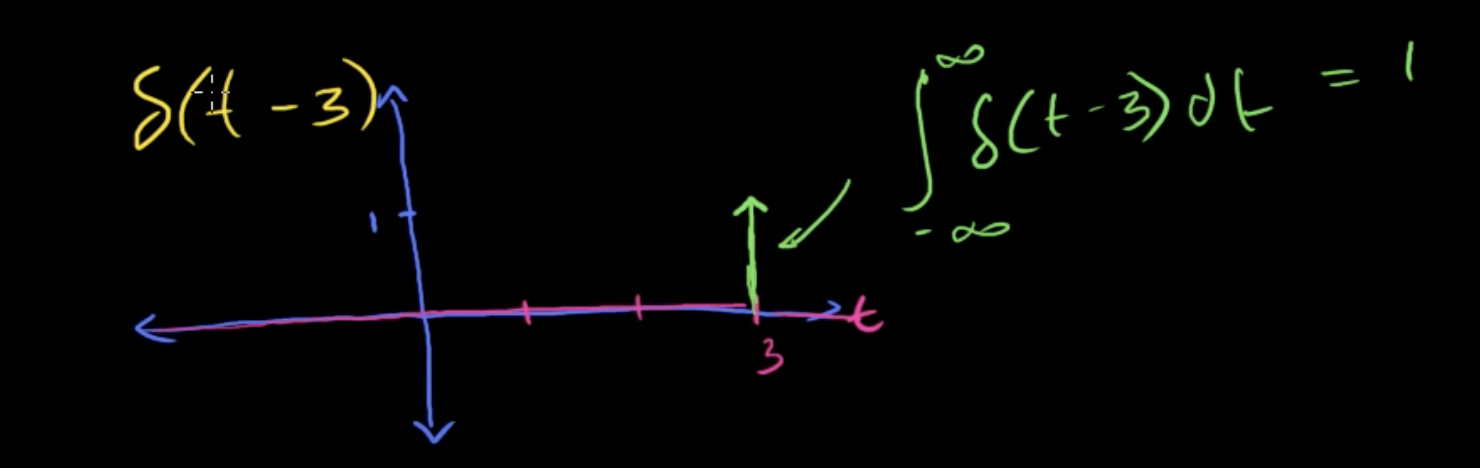
shifting of Dirac function
$\delta(t-3)$ means shifting the Dirac delta function to the right by 3, so the functions is infinity at t=3 and the integration (the area at that point) is still 1.
Laplace transform of the dirac delta function
Consider the Laplace transform of function: $ \delta (t-c)f(t) $ , according to the definition of Laplace transform,
$$ \mathscr{L} \lbrace \delta (t-c)f(t) \rbrace = \int_{0} ^{\infty} e^{-st}\ f(t)\ \delta (t-c)\ \ dt $$
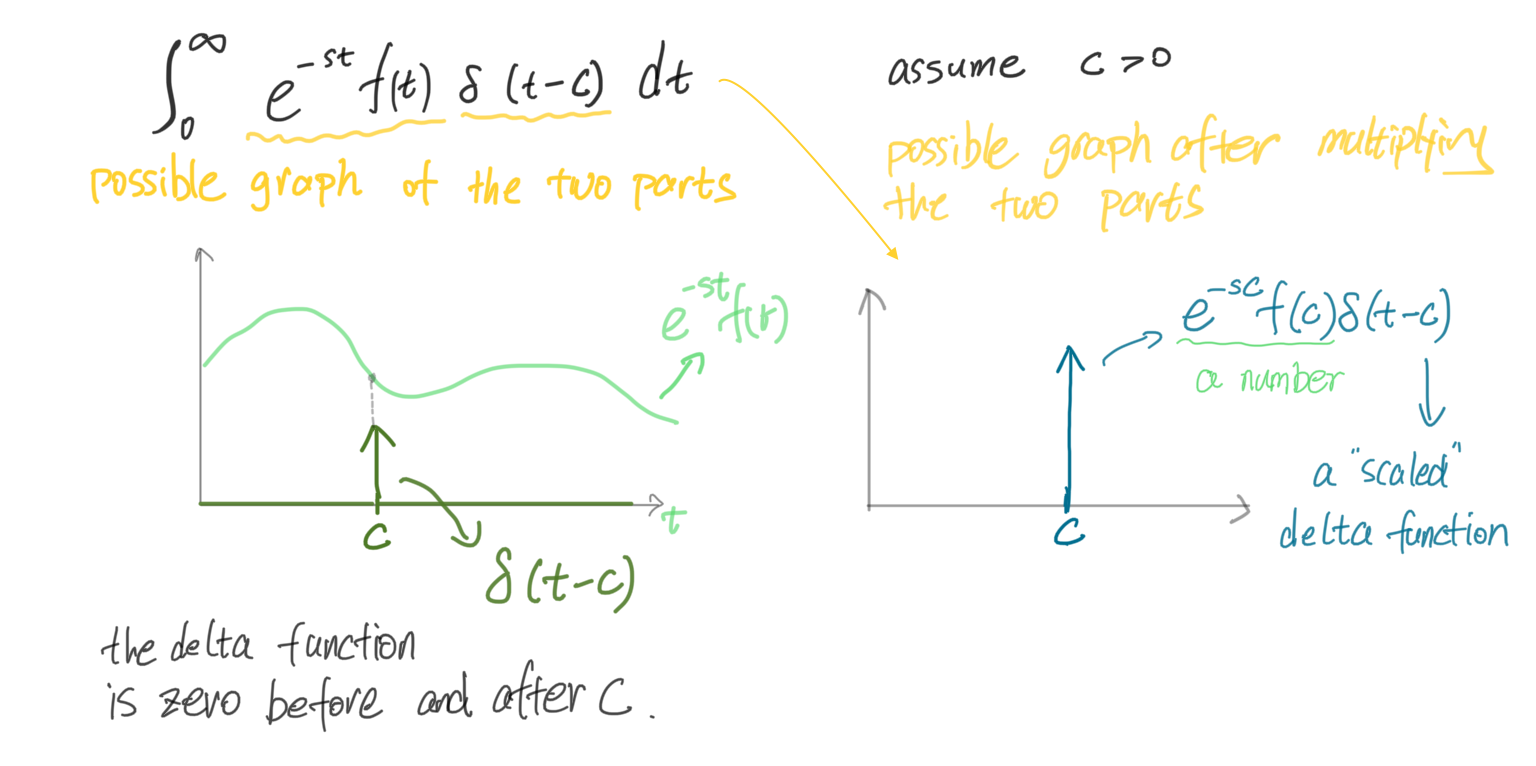
Therefore, the above integral expression is equivalent to
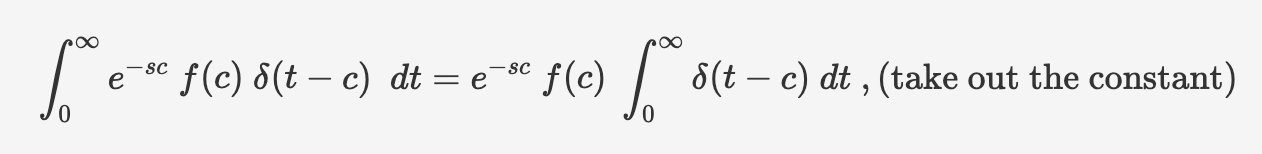
by definition, $\int_{0} ^{\infty}\delta (t-c)\ dt=1$ , therefore,
$$ \large \mathscr{L} \lbrace \delta (t-c)f(t) \rbrace = e^{-sc}\ f(c) $$
From this, we can get:
$$ \mathscr{L} \lbrace \delta(t)\rbrace=1\ \ \ [whereas\ c=0, f(t)=1] $$
$$ \mathscr{L} \lbrace \delta(t-c)\rbrace = e^{-sc} \ \ \ [whereas\ f(t)=1] $$
[========]
use Laplace transform to solve DE
for homogeneous DE
consider a differential equation:
$ y''+5y'+6y=0, y(0)=2, y'(0)=3 $
to use the Laplace transform here, we essentially just take the Laplace Transform of both sides of this equation.
$ \mathscr{L}\lbrace y'' \rbrace + 5\mathscr{L}\lbrace y' \rbrace + 6\mathscr{L}\lbrace y \rbrace=0$ .(0's Laplace transform is still 0.)
reference:
$\ \mathscr{L} \lbrace f'(t) \rbrace=s\mathscr{L} \lbrace f(t) \rbrace-f(0) $ .
$ \mathscr{L} \lbrace f''(t) \rbrace=s\mathscr{L} \lbrace f'(t) \rbrace-f'(0) $
so the three terms are equivalent to
$[s\mathscr{L} \lbrace y' \rbrace-y'(0)]+5[s\mathscr{L} \lbrace y \rbrace-y(0)]+6[\mathscr{L} \lbrace y \rbrace]=0 $
use the reference again to break down more derivatives.
$ [s(s\mathscr{L} \lbrace y \rbrace-y(0))-y'(0)]+5[s\mathscr{L} \lbrace y \rbrace-y(0)]+6[\mathscr{L} \lbrace y \rbrace]=0 \ \ \Rightarrow $ (substitute initial values)
$ s^2\mathscr{L} \lbrace y \rbrace -sy(0)-y'(0)+5s\mathscr{L} \lbrace y \rbrace-5y(0)+6\mathscr{L} \lbrace y \rbrace=$
$ (s^2+5s+6)\mathscr{L} \lbrace y \rbrace -2s-3-10=0 $
notice the coefficients of the polynomial of s are same as the coefficients in DE.
Now we can rearrange the equation to isolate the Laplace part.
$$ \mathscr{L} \lbrace y \rbrace =\frac{(2s+13)}{(s^2+5s+6)} $$
Now the problem became that to find the inverse of this Laplace transform.
$$ \mathscr{L} \lbrace y \rbrace =\frac{(2s+13)}{(s^2+5s+6)}=\frac{(2s+13)}{(s+2)(s+3)}=\frac{A}{s+2}+\frac{B}{s+3} $$
this simple fraction form is closer to some possible Laplace transform results we've already known.
$A(s+3)+B(s+2)=(A+B)s+(3A+2B)=2s+13$ , so $ A+B=2,\ 3A+2B=13 $ , then $A=9, B=-7$ .
from the calculation, we got
$$ \mathscr{L} \lbrace y \rbrace =\frac{9}{s+2}+\frac{-7}{s+3}=9\left(\frac{1}{s+2}\right)-7\left(\frac{1}{s+3}\right) $$
refer $ \mathscr{L} \lbrace e^{at} \rbrace= \frac{1}{s-a} $
therefore,
$$ \mathscr{L} \lbrace y \rbrace =9\mathscr{L} \lbrace e^{-2t} \rbrace-7\mathscr{L} \lbrace e^{-3t} \rbrace=\mathscr{L} \lbrace 9e^{-2t}-7e^{-3t} \rbrace $$
(Laplace transform is a linear operator.)
so we got $y=9e^{-2t}-7e^{-3t}$
for nonhomogeneous DE
consider a DE: $y''+y=\sin 2t \ , y(0)=2, y'(0)=1 $ .
Now take the transform for both side. First,
$ \mathscr{L} \lbrace y'' \rbrace = s^2\mathscr{L} \lbrace y \rbrace -sy(0)-y'(0)=s^2Y(s)-sy(0)-y'(0)$ , (the result of the transform is just a function of s), substitute the initial value:
$ s^2Y(s)-sy(0)-y'(0)=s^2Y(s)-2s-1$ , this the $ \mathscr{L} \lbrace y'' \rbrace$ part.
The Laplace transform of $y$ is just $ Y(s)$ , and the Laplace transform of $\sin 2t$ is $\frac{2}{s^2+4}$, therefore take the transform of both sides of the original DE will become
$ s^2Y(s)-2s-1+Y(s)=\frac{2}{s^2+4} \Rightarrow (s^2+1)Y(s)=\frac{2}{s^2+4}+2s+1 \ \Rightarrow $
$ Y(s)=\frac{2}{(s^2+4)(s^2+1)}+\frac{2s}{(s^2+1)}+\frac{1}{(s^2+1)}$
Now break up the first term into simpler fractions.
$ \frac{2}{(s^2+4)(s^2+1)}=\frac{As+B}{s^2+4}+\frac{Cs+D}{s^2+1}\ \ , (As+B)(s^2+1)+(Cs+D)(s^2+1)=(A+C)s^3+(B+D)s^2+(A+4C)s+(B+4D)= 2\ , A=0, B=-2/3, C=0,D=2/3 $
$ \frac{2}{(s^2+4)(s^2+1)}=\frac{-2/3}{s^2+4}+\frac{2/3}{s^2+1}=-\frac{1}{3}\left(\frac{2}{s^2+4} \right)+\frac{2}{3}\left(\frac{1}{s^2+1} \right) $ , therefore,
$ Y(s)=-\frac{1}{3}\left(\frac{2}{s^2+4}\right) + \frac{2}{3}\left(\frac{1}{s^2+1}\right)+2\left(\frac{s}{s^2+1}\right)+\frac{1}{s^2+1} $ ,
notice the fractions here are results of some cosine or sine's Laplace transform. Remember $Y(s)$ is the Laplace transform of $y$, so take the inverse to get $y$.
$ y(t)=-\frac{1}{3}\sin 2t+\frac{2}{3}\sin t+2\cos t+\sin t $
$\ \ \ \ \ \ \ \ =-\frac{1}{3}\sin 2t+\frac{5}{3}\sin t+2\cos t $ .
for DE involved step function
consider a differential equation which involved a step function:
$$ y''+4y=\sin t-u_{2\pi}(t) \sin(t-2\pi)$$
Initial value: $ y(0)=0, y'(0)=0$
still, take Laplace transform of both sides.
$$ s^2\mathscr{L} \lbrace y \rbrace -sy(0)-y'(0)+4\mathscr{L} \lbrace y \rbrace = \frac{1}{s^2+1}-e^{-2\pi s} \ \frac{1}{s^2+1}$$
reference: $ \mathscr{L} \lbrace u_c(t)f(t-c) \rbrace= e^{-cs}F(s) \ F(s) \textit{means the Laplace transform result of }f(t) $
then,
$$ \mathscr{L} \lbrace y \rbrace (s^2+4)=\frac{1-e^{-2\pi s}}{s^2+1} \Rightarrow \mathscr{L} \lbrace y \rbrace=(1-e^{-2\pi s})\frac{1}{(s^2+1)(s^2+4)} $$
again, we need to do some partial fraction expansion (same as the previous example). Therefore,
$$ \mathscr{L} \lbrace y \rbrace =(1-e^{-2\pi s})\left(\frac{1/3}{s^2+1}-\frac{1/3}{s^2+4} \right)$$
$$ =\frac{1}{3}\left(\frac{1}{s^2+1} \right)-\frac{1}{6}\left(\frac{2}{s^2+4} \right)-\frac{e^{-2\pi s}}{3} \left(\frac{1}{s^2+1} \right)+\frac{e^{-2\pi s}}{6}\left(\frac{2}{s^2+4} \right) $$
The pattern became straightforward, so it's ok to take the inverse now.
reference: $u_{2\pi}(t)f(t-2\pi)=e^{-2\pi s}F(s) $
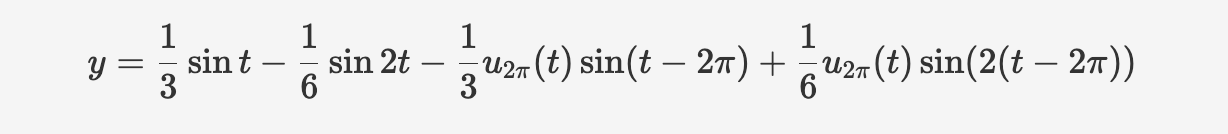
Part III
Convolution theorem
$$ \large (f*g)(t)=\int_0 ^t f(t-\tau)g(\tau) \ d\tau $$
for $ f(t)=\sin t,\ g(t)=\cos t $ , to convolution the two functions:
$ (f*g)(t)$
$ =\int_0 ^t \sin (t-\tau) \cos\tau\ d\tau $
$ =\int_0 ^t (\sin t \cos \tau-\cos t \sin \tau) \cos\tau \ d\tau $
$ =\int_0 ^t \sin t \cos^2 \tau-\cos t \sin \tau \cos\tau\ d\tau $
$ =\int_0 ^t \sin t \cos^2 \tau \ d\tau-\int_0 ^t \cos t \sin \tau \cos\tau\ d\tau $
( $\sin t$ and $\cos t$ are constants.)
$ =\sin t \int_0 ^t \cos^2 \tau \ d\tau-\cos t \int_0 ^t \sin \tau \cos\tau\ d\tau $
(use trig identity and u substitution. $\cos^2\tau=\frac{1}{2}(1+\cos 2\tau) ; $ set $ u=\sin \tau, du=\cos \tau\ d\tau $)
$$ =\frac{1}{2}\sin t \int0 ^t (1+\cos 2\tau)\ d\tau - \cos t \int{\tau=0} ^{\tau=t} u\ du $$
$$ =\frac{1}{2}\sin t \left| \tau+\frac{1}{2}\sin2\tau \right|0^t-\cos t \left| \frac{1}{2}u^2 \right|{u=0}^{u=\sin t} $$
$$ =\frac{1}{2}\sin t \left(t+\frac{1}{2}\sin2t-0-0 \right)-\cos t \left(\frac{1}{2}\sin^2t-0 \right) $$
($\sin 2t=2\sin t \cos t $)
$$ =\frac{1}{2}t\sin t+\frac{1}{4}\sin t \sin 2t-\frac{1}{2}\sin^2 t\cos t $$
$$ =\frac{1}{2}t\sin t+\frac{1}{4}\sin^2 t \cos t -\frac{1}{2}\sin^2 t\cos t $$
$$ = \frac{1}{2}t\sin t-\frac{1}{4}\sin^2 t \cos t $$

