本课程是MITx在线数学课之一,是系列课程XSeries in 18.03x Differential Equations的第一个,也是学习后续高阶课的必修基础课,名为Introduction to Differential Equation 代号18.031x。整个系列未看到中文版。课程由来自麻省理工、普林斯顿等大学的多位教授、研究人员设计制作, 是一套非常棒的课程,内容丰满、制作精良。18.031x共有五个单元。本系列博客是经过我自己翻译后的中文笔记。
$$ \Large Unit\ 2: Complex\ Exponentials\ and\ ODEs $$
lecture 3 Introduction to Complex Numbers
$ z=a+bi $, z的实部是a,z的虚部是b。关于z的基本性质有:
$$ Re\ z=\frac{z+\overline{z}}{2}, \ Im\ z=\frac{z-\overline{z}}{2i} $$
$$ \overline{\overline{z}}=z, \ z\overline{z}=|z|^2 $$
极坐标形式
$ a+bi=(rcos\theta)+(rsin\theta)i=r(cos\theta+isin\theta)$
$ r=|z| $
在工程领域,r=1的复数常写成$ e^{i\theta} $, 即欧拉公式:
$$ e^{i\theta}=cos(\theta)+isin(\theta) $$
【注意】 $ e^{i0}=cos(0)+isin(0)=1 $
指数微分
$$ y=e^{ax}, \ \ \ \frac{dy}{dx}=ay $$
$\ e^{it} $ 同样满足这一规律, $\frac{d}{dt}e^{it}=ie^{it} $ (下面欧拉公式部分有证明过程)。
把复数写成e指数的形式有很多好处,尤其在计算上变得很方便:

lecture 4 The Complex Exponential Function
复指数的定义方式之一:根据上面指数微分的规律,复指数函数$e^{zt}$是$y'=ay$这类微分方程的一个解。
$$ \frac{d}{dt}e^{zt}=z e^{zt},\ e^{z0}=1,\ \ \ z为复数,t为实变量 $$
复指数的运动轨迹
EXAMPLE
考查$ e^{(-5-2i)t}=e^{-5t}e^{i(-2t)} $,当t趋向无穷时,曲线上的点的运动轨迹是顺时针螺旋向内的。
当t趋向无穷时,复指数的模$|e^{-5t}|$趋向零,所以运动点向内走。
argument角度为$-2t$, 是下降趋势,所以运动点是顺时针方向。
复数的n次方根
EXAMPLE
求$z^5=-32$的复数解。
将z表示为$re^{i\theta}$的形式:
$$ (re^{i\theta})^5=32e^{i\pi} $$
$ r^5=32,\ 5\theta=\pi+2\pi k $
因此,$ z= 2e^{i\frac{1}{5}(\pi+2\pi k)} $
k取0~4,就是五个复数解,从极坐标上看就是从$\frac{\pi}{5}$ 开始旋转,每次转$\frac{2\pi}{5}$所得的五个角度。

复数值函数 complex-valued function
复数值函数可以表示为: $y(t)=f(t)+ig(t) $ ,t为实自变量,其中的$f(t)$和$g(t)$均为关于t的实数值函数。(这一形式显然是在为复指数做准备,因为等式右边正是欧拉公式右边的pattern) 显然,$f(t)$是这个函数的“实部”,$g(t)$则是其“虚部”,可以表示为:
$$ f(t)=Re\ y(t), \ \ g(t)=Im\ y(t) $$
它的微分和积分,都可以按照实部和虚部分开计算:
$$ y'(t)=f'(t)+ig'(t), \ \ \ \int{y(t)}=\int{f(t)}+i\int{g(t)} $$
EXAMPLE
$ y=\frac{2+3i}{1+it} $ , 利用共轭将分母有理化并整理成 $y(t)=f(t)+ig(t)$ 的形式,从而就可以得到y的实部与虚部:
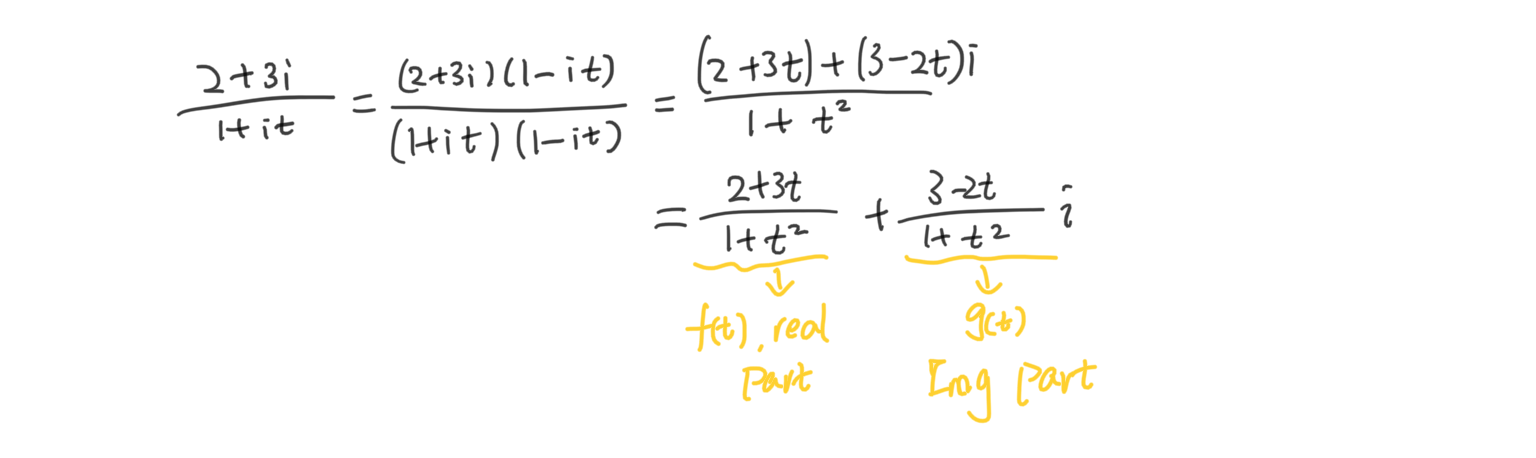
复数值函数的基本属性
指数 $e^t$ 的基本属性同样适用于复指数 $e^z$ (z is complex number) 。
证明这条辅助定理:对于任意复数 $\alpha,\beta$ , $e^{\alpha t}e^{\beta t}=e^{(\alpha + \beta)t} $ .
要证明这两个函数相等,也就是说证明这两个函数实为一个函数。前面对复指数有一个基于微分的定义:复指数函数$e^{zt}$是$y'=ay$这类微分方程的一个解。 并且在给出特定初始值的情况下,微分方程有且仅有一个解。因此,用以下思路来证明:
证明 $e^{\alpha t}e^{\beta t} \ 和\ e^{(\alpha + \beta)t} $ 都是 $ y'=(\alpha + \beta)y, \ \ y(0)=1 $ 的解,由于解的唯一性,这两个复指数函数必为同一个函数。
$ e^{(\alpha + \beta)t} $ 这个函数的形式完全符合上面的微分方程,同时也满足初值,因此可以直接判定它是这个微分方程的解。另一个复指数求其导函数并代入初始值:
$$ y'=(\alpha e^{\alpha t})e^{\beta t}+e^{\alpha t} (\beta e^{\beta t})=(\alpha + \beta)e^{\alpha t}e^{\beta t} =(\alpha + \beta)y $$
代入y(0)结果等于1,符合初始值。同样证明了这个复指数函数是微分方程的解。由于解的唯一性,两个复指数函数必为同一个函数。
欧拉公式
利用复指数的定义和微分方程证明欧拉公式 $ e^{it}=cost+isint $ :
根据复指数的基本定义,$ e^{it} $ 是 $ y'=iy, \ y(0)=1 $ 的解,等式左边无需再证明。接下来对等式右边求导:
$$ \frac{d}{dt}cost+isint=-sint+icost=i(isint+cost) $$
表面$cost+isint$也是 $ y'=iy, \ y(0)=1 $ 的解,根据唯一解理论,二者相等。
$ e^{it} $ 的运动轨迹
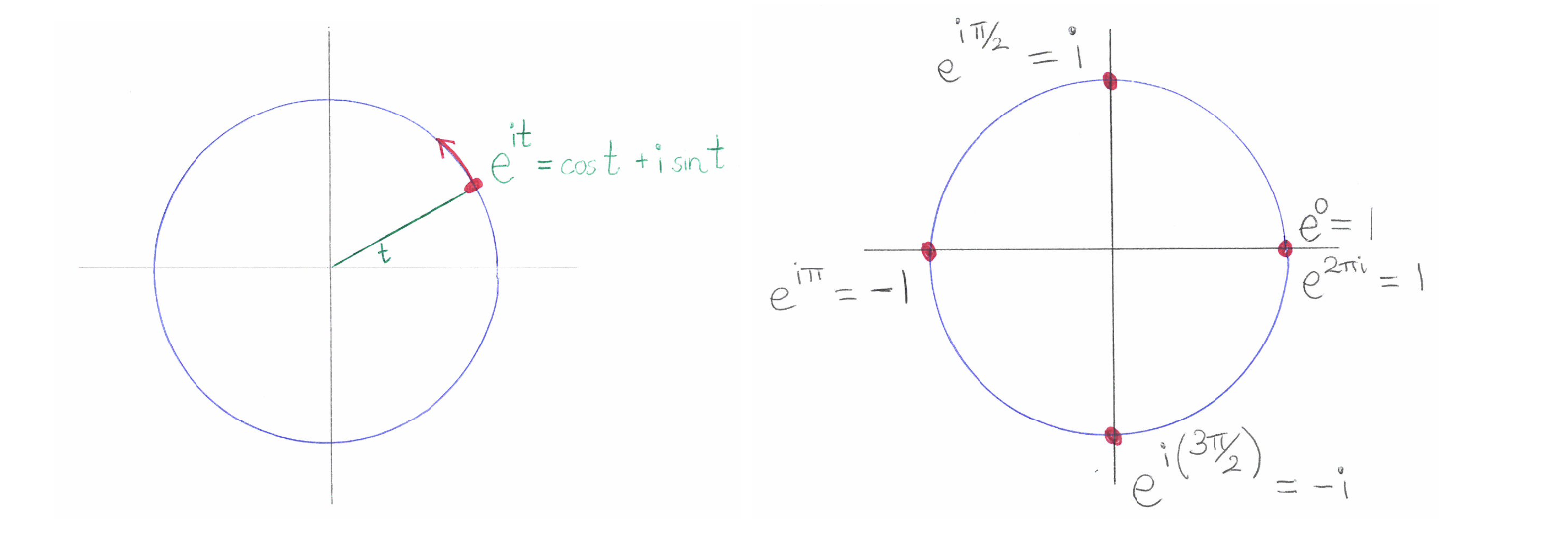
随着t增大,复数$ e^{it} $ 会朝着逆时针方向运动,其运动轨迹正是单位圆的圆周。
复指数常用等式
$$ e^{a+bi}=e^{a}cosb+isinb, \ \ \ (a,b为任意实数) $$
$$ e^{-it}=cost-isint=\overline{e^{it}} \ \ \ (t为任意实数) $$
$$ |e^{it}|=1 \ \ \ (t为任意实数)$$
复平面极坐标
非零复数 $z=x+yi$ ,
$$ x+yi=(rcos\theta)+(rsin\theta)i=r(cos\theta+isin\theta)=re^{i\theta} $$
$re^{i\theta}$ 被称为复数z的极坐标形式,$r=|z|=\sqrt{x^2+y^2}$ .
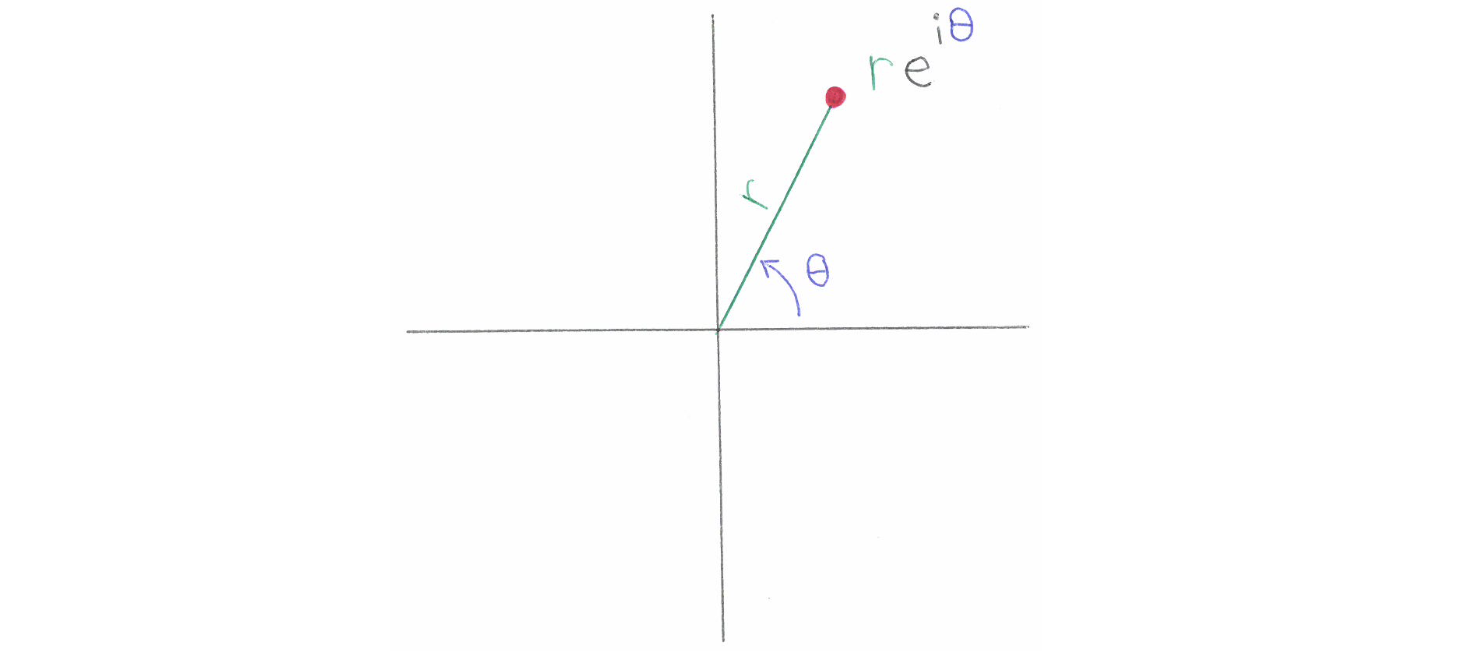
$\theta$ 被称为复数z的幅角。$\theta=Arg z=arctan(y/x)$
旋转笑脸
EXAMPLE
把一个复平面中的笑脸乘以3i(即笑脸图中的每个点都乘以3i)后会怎样?
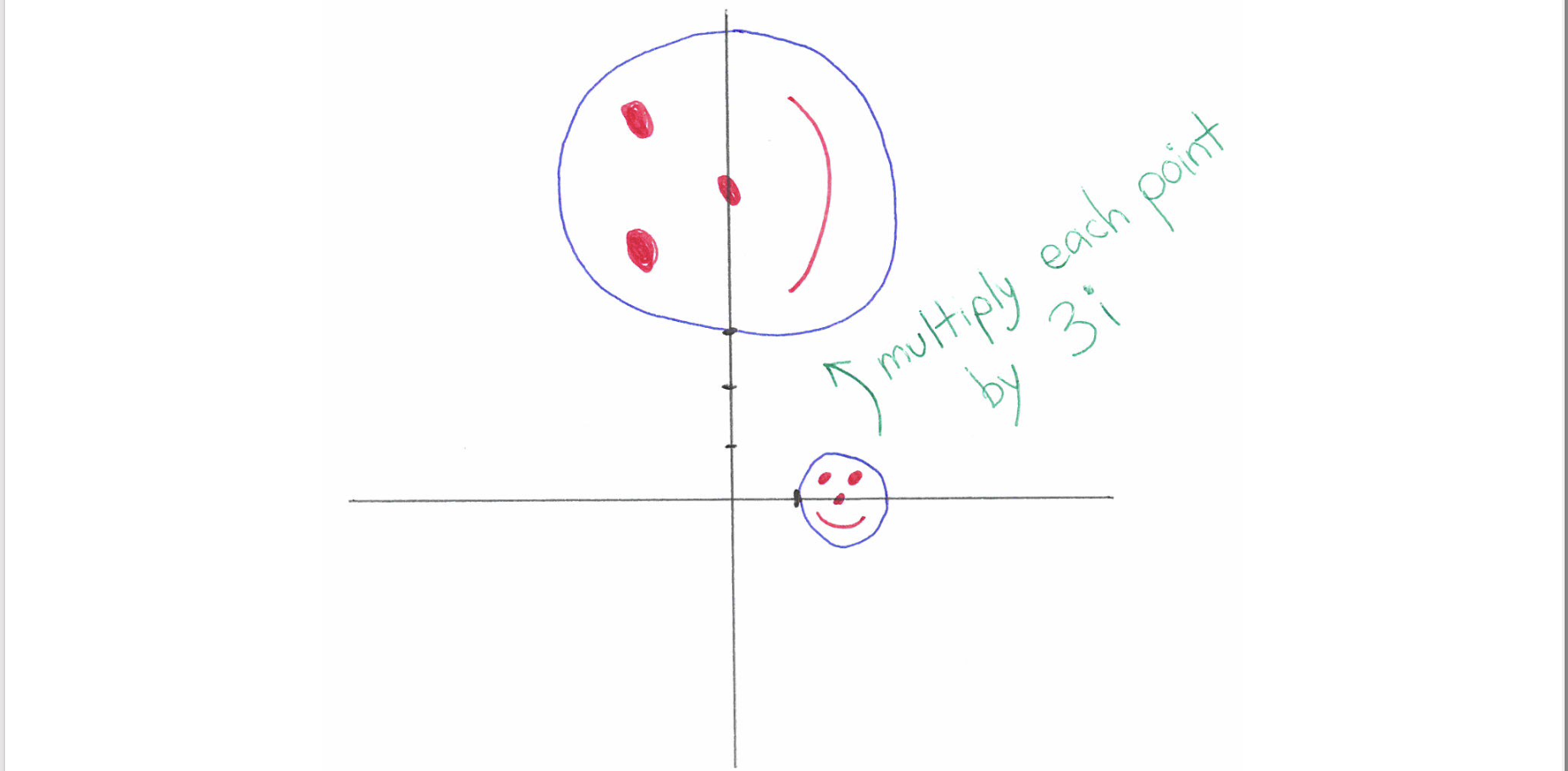
既然是做乘法,就要考虑极坐标形式。$ i=e^{i\pi/2},\ (i=0+1i,可知\ r=1, \theta=\pi/2) $ 。乘以一个i就意味着逆时针(正向)旋转90度,为什么是90度?这就是极坐标形式的优点,极坐标明确而直接地告诉我们这个复数的argument就是$\pi/2$ . 而乘以一个常数则意味着简单的伸缩(dilate),这道题是乘以3,所以每一点的坐标值都乘以3,相当于拉伸为原来的3倍。比如鼻子那个点,原来是在接近(2,0)的位置,它被乘以3i之后,就到了差不多接近(0,6i)的位置。
如果把它看作一个(类似向量性质的)复数,这家伙的模本来是差不多2,现在的模就是差不多6.
复指数函数e^(a+bi)t
非常重要的函数 $\Large e^{(a+bi)t}$ , 将函数可视化且支持互动的在线工具:复指数函数互动工具
随着t增大,$(a+bi)t$会沿着一条过零点的直线运动,而 $e^{(a+bi)t}$ 上的点可能是沿着某一段直线、或者圆、或者螺旋线运动,取决于a和b的值。
example
考察函数 $e^{(-5-2i)t}$ 当t趋向正无穷,函数的运动轨迹。
将函数整理为标准的极坐标形式: $e^{(-5-2i)t}=e^{-5t}e^{i(-2t)} $,可见模(绝对值)为 $e^{-5t}$ ,随着t增大,模将趋向零;从 $e^{i(-2t)} $ 可知,复数的幅角为-2t,随着t增大,幅角是逐渐降低的,也就是反向旋转(顺时针)。因此这个函数的运动轨迹是顺时针螺旋向内。
e^it, e^-it作为cos与sin的线性组合
$e^z$ 这种形式往往有更好用的计算属性,所用常用来替代cos、sin,反过来,cos、sin也可视作复指数的实部与虚部。
$$ e^{it}=cost+isint, \ \ \ e^{-it}=cost-isint $$
$$ cost=\frac{e^{it}+e^{-it}}{2}, \ \ \ sint=\frac{e^{it}-e^{-it}}{2i} $$
很多时候,自变量不是直接的t,而是$\omega t$:
$$ e^{i\omega t}=cos\omega t+isin\omega t, \ \ \ e^{-i\omega t}=cos\omega t-isin\omega t, \ \ \
cos\omega t=\frac{e^{i\omega t}+e^{-i\omega t}}{2}, \ \ \ sin\omega t=\frac{e^{i\omega t}-e^{-i\omega t}}{2i} $$
lecture 5 Homogeneous 2nd Order Linear ODEs with Constant Coefficients
弹簧振荡系统 p1
弹簧一端固定在墙上,一端连着一个小车;小车的另一端带动一个阻尼系统。各变量和单位如下:
t:时间(秒)
x:位移(米),x=0为平衡位置,弹簧不施加作用力。
m:小车的重量(kg)
$F_{spring}$: 弹簧作用于小车的力(N)
$F_{dashpot}$:阻尼作用于小车的力(N)
$F_{external}$:外部力(N)(比如人推小车)
t是独立变量,其他是关于t的函数。
从一般的物理常识可知,弹簧的力是关于x的函数,与位移方向相反;阻尼的力是关于速度($\dot{x}$)的函数。这些关系可以简要的用线性函数来估算。 根据Hooke's law,$ F_{spring}=-kx $;而阻尼作用力 $ F_{dashpot}=-b\dot{x} $, 其中k是弹簧系数,b是阻尼系数, k,b都大于零。根据牛顿第二定律:F = F_spring + F_dashpot + F_external
因此,$ m\ddot{x}=-kx-b\dot{x}+F_{external} $
于是得到一个二阶线性ODE。有时候写成:$ \large m\ddot{x}+kx+b\dot{x}=F_{external}(t) $ .如果没有外力,等式右边就就等于0。当然这不是标准式,因为第一项系数不为零。这个模型是所有振荡系统的基础模型。
用系统与信号的语言来描述就是,输入:外力;系统:弹簧、阻尼和物块构成的体系;输出:位移x(t).
现在假设一种最简易的情况,m=k=1, 并且没有阻尼和外部作用力,只有一个物块和弹簧:
$$ \ddot{x}+x=0 $$
这个ODE每一个解都对应一个特定的初值情况,反过来,每一种特定初值情况下,有且仅有一个解。观察这个方程,猜测可能的解以及对应的初值。
- $ cos(t) $ 是方程的一个解,且$ x(0)=1, \dot{x}(0)=0 $;
- $ sin(t) $ 是方程的一个解,且$ x(0)=0, \dot{x}(0)=1 $;
- $ cos(t)+sin(t), 3sin(t), 0, -2cos(t) $ 都是可能的解。
cos与sin的任意线性组合,都是原方程的解,表示为:$ c_1cos t+c_2sin t $.
线性齐次ODE叠加性 superposition
对于一个n阶线性齐次微分方程:$ pn(t)y^{(n)}+p{n-1}(t)y^{(n-1)}+...+p_1(t)y'+p_0(t)y=0 $ , 有这样的特征:
- 零函数0是一个解;
- 任意某个解的倍数(乘上一个常数系数)仍是方程的一个解;
- 任意两个解相加能得到另一个方程的解。
总之,$ \large 方程任意解的任意线性组合能得到方程的解。$ 所有这些解最终将构成所谓的“向量空间”。
二阶线性齐次ODE
接续前面的方程的解 $ x(t)=c_1cos t+c_2sin t $ , 对于任意c1,c2的值,都能得到一个方程的解,实际上这个2参数的函数集表达的正是原微分方程的全部解,因此也称“一般解”。
对于任意一个二阶的线性齐次微分方程,函数集 $ x(t)=c_1x_1(t)+c_2x_2(t) $(其中x_1, x_2分别都是这个二阶DE的解, c_1,c_2可以是任意常数) 是原方程的一般解。
$\large 注意: x_1, x_2$ 必须是线性独立的,不然就等同于一个解了,当然也不能为零。这两个解可以说是构成所有解集合的基本元素。
由此,求解一个二阶线性ODE的问题就简化成了只需要找到两个线性独立的解。
二阶的DE需要一个有2个参数的函数集,这背后是有必然逻辑的,大体上可以理解为,需要进行两次积分,每次都会出现一个任意常数。实际上,n阶的DE就会需要一个有n个参数的函数集。
既然这个函数集有两个未知参数,那么很显然,如果需要明确知道一个特定解,就需要知道两个数据。实际上,一般在初始起点,都会获得两个初值:$ y(0), \dot{y}(0) $, 或者其他某个非零的起点。
比较一阶的线性ODE,作为一般解的函数就只有一个参数,寻求特解时,也只需一个初始值。
特征方程求解
如何求解$ m\ddot{x}+b\dot{x}+kx=0 $ ?
直接带入$x=e^{rt}$ 然后尝试求解r,这是一种基于经验而来的惯用方法,仅限于线性ODE。
$\dot{x}=re^{rt}, \ \ddot{x}=r^2e^{rt} $, 于是,这个ODE就可以写成:
$$ mr^2e^{rt}+bre^{rt}+ke^{rt} =0 $$
提取公因式并除掉永不为零的指数部分,得到:
$$ mr^2+br+k = 0 $$
$ \large mr^2+br+k $ 被称为原ODE的特征多项式, 可记为 $p(r)$,于是 $p(r)=0 $就被称为特征方程。
比如,前面那个简易版的弹簧模型 $ \ddot{x}+x=0 $ ,它的特征方程就是 $r^2+1=0$
一个2次方程的根有可能是两个不同的实数解or复数解,也可能是两个相同的解,这里只关注不同解的情况:
-
一,两个不同的实数解,其一般解就是简单的带有两个系数的线性组合形式:$ c_1e^{r_1t}+c_2e^{r_2t} $.
-
二,两个不同的复数解,复数解都是成对出现的,即$r=a\pm bi $,所以一般解表示为:$c_1e^{(a+bi)t}+c_2e^{(a-bi)t}$,这两个共轭复指数构成了“基本解”(解集合空间中的basis)。而对于实系数ODE,复指数(共轭中的任何哪个都一样)的实部和虚部也同样是原ODE的解,并且也是构成解空间的basis。
$$ e^{(a+bi)t}=e^{at}e^{ibt} \Rightarrow Re\ e^{(a+bi)t}= e^{at}cos(bt), \ Im\ e^{(a+bi)t}=e^{at}sin(bt) $$
与复指数解的最大不同就是,这两个解都是实数,同时它们也线性独立,从而构成解空间。
之所以复指数函数的实部与虚部能够成为基本解,正是因为上一节lecture 4最后一部分总结的,复指数本质上就是余弦、正弦的线性组合。
什么时候用实函数?复指数很多时候计算起来是方便的,但在处理现实物理问题时,复数不适用,我们需要的是实函数。
所以,复数解总结为:
$\clubsuit$ IMPORTANT THEOREM: 如果$u+iv$(u和v都是关于t的函数)是某个ODE -- $\ddot{y}+A\dot{y}+By=0 $ 的复函数解,那么u和v,也就是$\large实部和虚部$就分别是我们需要的$\large两个基本实函数解$ (实部和虚部的线性组合就是一般解)。这个理论的前提是$特征方程的系数均为实数$。
实数解例题
$\diamondsuit$ example 求 $ \ddot{y}+5\dot{y}+6y=0 $ 的一般解.
基本方法:$ e^{rt}$ 是一个解(r作为特征方程的根)。
先写出它的特征方程:
$$ p(r)=r^2+5r+6=0=(r+2)(r+3) ,\ \ r=-2, -3 $$
可知,$e^{-2t}, e^{-3t} $ 是两个基本解,因此,这个DE的一般解为:
$$ c_1e^{-2t}+c_2e^{-3t}, \ (c_1,c_2 为任意常数) $$
满足初值 $y(0)=0, \dot{y}(0)=1 $ 的特解是什么?
直接带到一般解式子中,得到:$ c_1+c_2=0, -2c_1-3c_2=1 $ , 得到 $c_1=1, c_2=-1 $ ,因此特解为:$ e^{-2t}-e^{-3t} $ .
$\diamondsuit$ example 求解$ \ddot{x}+5\dot{x}+4x=0 $ .
特征方程为$r^2+5r+4=0 $, 求得$ r=-1, -4$. 一般解可以写成:
$$ x(t)=c_1e^{-t}+c_2e^{-4t} $$
复数解例题
$\diamondsuit$ example 求解$ \ddot{x}+4\dot{x}+5x=0 $ .
特征方程为$r^2+4r+5=0$,用二次方程解的公式求得$r=-2\pm i$, 所以基本解为:
$$ z(t)=e^{(-2+i)t} \ \ , \ \overline{z}(t)=e^{(-2-i)t} $$
一般解就是这两个基本解的线性组合,但对于系数均为实数的ODE,我们只关注实函数。复指数可以写成$ e^{(-2+i)t}=e^{-2t}cost+ie^{-2t}sint $, 其实部为$e^{-2t}cost$,虚部为$e^{-2t}sint$. 一般解就是这两个基本解的线性组合:
$$ x(t)=c_1 e^{-2t}cost+c_2e^{-2t}sint $$
用z的共轭也可以求,所得结果是一样的。 (用cos、sin所表示的一般解与用复指数表示的一般解是等效的,它们代表了相同的“空间”,后续做验证。)
前面的无阻尼弹簧振荡系统 $ \ddot{x}+x=0 $,按照特征方程求解,可知 $r^2+1=0, r=\pm i $, 因此,它的基本解就可以写成 $e^{it}, e^{-it} $, 对于实际物理问题,我们使用实函数,找到这个复指数的实部和虚部,就可以将一般解写出来:$c_1cost+c_2sint $ . 前面已经知道这两个解,之前是直接尝试将两种三角函数带入原式,发现它们的确是方程的解,而且线性独立,于是可以通过线性组合构成解空间。
总结来说,假设$y(t)$表示复函数(t为实变量),若$y$和 $\overline{y}$ 是某二阶齐次线性DE(实系数)的基本解,那么其实部和虚部(直接以$Re(y),Im(y)$ 替代$y$和 $\overline{y}$),将构成新的实函数基本解,它们构成的一般解(即所有线性组合)将给出原ODE的全部实解。
弹簧振荡系统 p2
还是之前那个系统,假设物块质量m=1(kg), 弹簧系数k=16(N/m 牛顿/米), 其位移x(t)符合DE:$ \ddot{x}+b\dot{x}+16x=0 ,\ b>0$ ,考察阻尼常数b的值对DE的解的影响。
a 特征方程及求解
-
DE的特征方程是什么?
$r^2+br+16=0$ -
如果特征方程的根是实数且不重复的,b应该取什么样的值?
r的值可以用二次方程解的公式表示出来:$r=-\frac{b}{2}\pm\frac{\sqrt{b^2-64}}{2} $ 决定二次方程根的特征的正是根号下的部分。若要取得实数根且无重复,需要$b^2-64>0$, 同时,已知b>0,所以,需要b>8。 -
在这个区间内的b,x的解(指数形式)可以表示为:
$$ x_1=e^{\frac{-b-\sqrt{b^2-64}}{2}t} , \ \ x_2=e^{\frac{-b+\sqrt{b^2-64}}{2}t} $$
b 初值情况
在符合以上条件的情况下,现给出一个初值情况,t=0时,中间的物体在平衡点右侧1米的位置,同时以$\frac{b}{2}(m/s)$的速度向左移动(设定位移x>0为正向),写出x(t)的表达式。(也就是求系数写出特解)
根据题意,初值情况实际上就是给出了 $x(0)=1 \ 和\ x'(0)=-\frac{b}{2} $
详细计算过程见图:

c 跨越几次平衡点
仍是基于前面的b的条件,方程有两个独立的实函数解的情况。考察物体会跨越平衡点(即x=0)多少次?(换句话说,在哪些可能的时间点,x(t)=0。也就是求x(t)=0时,t的值)
考察$c_1x_1+c_2x_2=0$, 即$ c_1e^{r_1t}=-c_2e^{r_2t} $, c是任意常数,因此可以简单表达为$ e^{r_1t}=ce^{r_2t} $, 假定c>0,式子两边取自然对数,得到$ r_1t=lnc+r_2t \Rightarrow t=\frac{lnc}{r_1-r_2} $. t的这个表达式显然是一个简单的一元线性方程,因此,t只能存在一个特定解,即物体跨越平衡点1次。但这还不是全部的情况。
在使用c这个系数时,是对系数的简化替代,实际上取 $ c=-\frac{c_2}{c_1} $,这里默认$ c_1\neq0 $, 同时还假定c>0, 即$ \frac{c_2}{c_1}<0 $. 现考察其他情况:
-
c>0, 即$ \frac{c_2}{c_1}<0 $
- 当$c_1=0, c_2\neq0, \ x(t)=c_2e^{r_2t} $ 指数恒大于0,所以这里x(t)=0是无解的,也就是不会跨越平衡点。
- 当$c_1\neq0, c_2=0, \ x(t)=c_1e^{r_1t} $ 和上一个同样道理,是无解的。
-
当c<0, 即$ \frac{c_2}{c_1}>0 $
这时,c2和c1的符号相同且都不为零。$ e^{r_1t}=ce^{r_2t} $中, 指数都恒大于0,c又小于0,显然无解,也是不会跨越平衡点。 -
当$c_1=c_2=0$, x(t)=0, 这等于整个系统没有动,物体就待在平衡点,而非“跨越”平衡点,这种情况并不在讨论范围内。
因此,要么跨越0次,要么跨越1次,这覆盖了全部的情况。
d 非实解的情况
- 如果特征方程的根为复数,b的值是多少(b>0)? 这就意味着根号下的部分小于零,$b^2-64<0$ ,因此b<8.
- 在同样的初值情况下(t=0时,中间的物体在平衡点右侧1米的位置,同时以$\frac{b}{2}(m/s)$的速度向左移动),且特征方程有两个不同的复函数解,找到满足初值的实函数表达式。

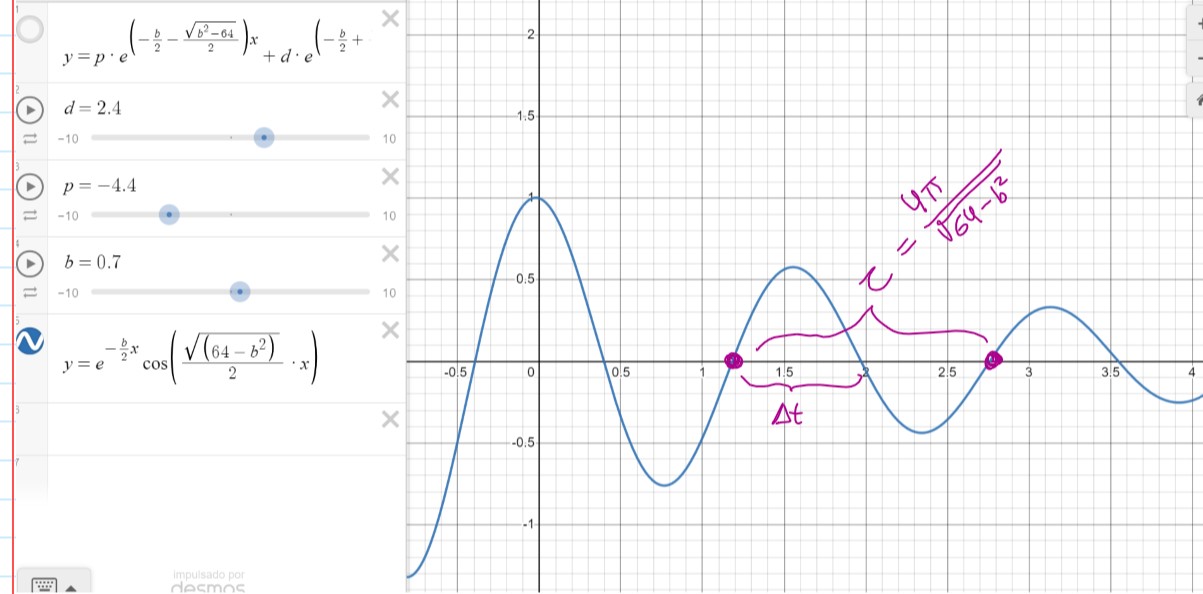
e 振荡周期
考察物体振荡的拟周期表达式$\tau$,一个周期等同于每次物体回归平衡点的间隔时间再乘以2,计算这个$\tau$:
上题已得出下x(t)的表达式$ e^{\frac{-bt}{2}}cos(\frac{\sqrt{64-b^2}}{2}t) $, 已知余弦周期是$2\pi$,所以可以马上找到这个以t为变量的cosine周期,直接用$2\pi$除以t的系数,得到:$\frac{4\pi}{\sqrt{64-b^2}}$. 课程论坛,TA给出了更为落地的朴素解法:

Homework A&B 摘录
Homework A
4-2: 当实数t趋近$+\infin,te^{-3it} $在复平面中的运动轨迹是怎样的?
$ e^{-3it} $是一个极坐标形式的复数,并且$ r=1, \theta=-3t $,所以这个复数沿着单位圆顺时针旋转。乘上一个大于0的实数t,改变了它的模,即$|te^{-3it}|=t $, 所以旋转过程还伴随着辐射半径的增长,因此这个复数的运动轨迹是顺时针向外延展的螺旋。
4-3: 用常数x和y表示$|\frac{1}{e^{x+yi}}|$, 即用x、y表示这个复数的模。
$$ \frac{1}{e^{x+yi}}=e^{-x-yi}=e^{-x}e^{-yi} $$
表示成$re^{i\theta}$的形式后,就一目了然了。e前的系数就是r,也就是模长。所以$ |\frac{1}{e^{x+yi}}|=e^{-x} $
4-6: 计算$(1+i\sqrt{3})^6 $.
乘除运算首先把复数从直角坐标形式转换成极坐标形式。$ r=2,\ \theta=arctan(\sqrt{3})=\pi/3 $, 因此 $1+i\sqrt{3}=2e^{\pi /3} $ ,原式改写为$ r^6e^{i6\theta} $ 的形式,$r^6=64$,$6\theta=2\pi \ \Rightarrow \ 64e^{i2\pi}=64(cos2\pi + isin2\pi )=64 $
Homework B
复指数函数

二阶ODE应用题 厨房门
厨房门可以双向摆动,一旦打开让其晃动,它可以自由地来回摆动,这很危险,因此在门上装了一个阻尼器。阻尼器满足微分方程 $ m\ddot{x}+b\dot{x}+kx=0 $ ,阻尼器参数:m=0.5, b=1.5, k=0.625.
- 这个DE的特征多项式是什么? $ 0.5r^2+1.5r+0.625 $
- 找到满足初值 $x(0)=x_0, \dot{x}(0)=v_0 $ 的特解。

-
在什么样的初值条件下,方程的解是一个指数$ce^{rt}$而非多个指数相加的形式($x_0, v_0的值或者之间的关系$)?
已知方程的通解是 $c_1x_1+c_2x_2$ 的形式,如果是只有一个指数,也就是只有其中的 $x_1$ 或者 $x_2$,这就意味着,其中一个的系数c为零。(决定系数c是多少的,正是具体的初值情况,这也是上一道题的意义)
上一小题已经得出两个系数用两个初值表达的式子,当 $c_1=0.5v_0+1.25x_0=0 $ 或者 $c_2=-0.5v_0-0.25x_0=0 $ 其中一个为零,就符合本题的情况。计算可得:$ x_0=-0.4v_0, \ \ x_0=-2v_0 $. -
假设 $x_0=0.25$, $v_0$应该是什么样的取值,使得以下描述会发生:当门一旦被松开,它会路过关闭位置(平衡点),然后又从那一边摆动回来。
整个过程从t=0开始,在之后的某一个时间点t,位移为零(平衡位置),即 $x(t)=0 $, 考察系数的取值情况,再根据以初值符号表示的系数的表达式以及给出的初始x值,查看初始速度可能的取值区间。

